Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Practice Problems
\(\textbf{1)}\) Acute, Obtuse, Right or Straight?
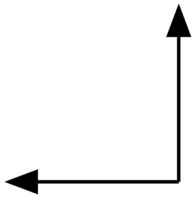
\(\textbf{2)}\) Acute, Obtuse, Right or Straight?

\(\textbf{3)}\) Acute, Obtuse, Right or Straight?
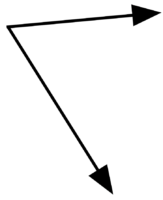
\(\textbf{4)}\) Acute, Obtuse, Right or Straight?
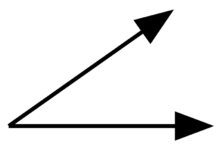
\(\textbf{5)}\) Acute, Obtuse, Right or Straight?
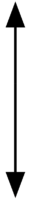
\(\textbf{6)}\) Acute, Obtuse, Right or Straight?
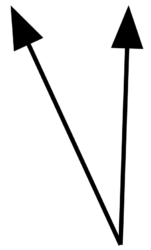
\(\textbf{7)}\) Acute, Obtuse, Right or Straight?
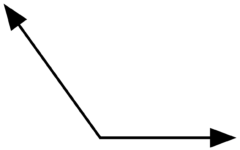
\(\textbf{8)}\) Acute, Obtuse, Right or Straight?
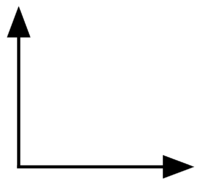
\(\textbf{9)}\) Acute, Obtuse, Right or Straight?
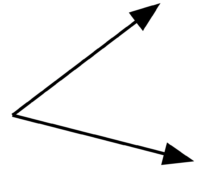
\(\textbf{10)}\) Acute, Obtuse, Right or Straight?
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Adjacent Angles}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Angle Addition Postulate}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Complimentary and Supplementary Angles}\)
\(\,\,\,\,\,\,\,\,\)
In Summary
In geometry, angles are classified by their size. Here are the main categories of angles:
Acute angles: These are angles that measure less than 90 degrees. An angle that measures exactly 90 degrees is called a right angle.
Obtuse angles: These are angles that measure more than 90 degrees but less than 180 degrees.
Straight angles: These are angles that measure exactly 180 degrees.
Reflex angles: These are angles that measure more than 180 degrees but less than 360 degrees.
Full angles: These are angles that measure exactly 360 degrees.
Classifying angles by size is typically covered in a geometry or trigonometry course. These topics are typically introduced in middle school or high school math classes, although they can also be covered in lower-level college math courses. In geometry, students learn about the properties and characteristics of angles, including how to classify them by size and measure them using a protractor.
In ancient Greek mathematics, the term “acute angle” was used to describe an angle that measured less than a right angle, while the term “obtuse angle” was used to describe an angle that measured more than a right angle. The terms “acute” and “obtuse” come from the Latin words “acutus” and “obtusus,” which mean “sharp” and “blunt,” respectively. These terms were chosen to describe the angle because the sharp end of a spear or sword is more acute, while the blunt end is more obtuse.
Real-world examples using angles
Construction: In construction, it’s important to know the size of angles in order to ensure that structures are stable and safe. For example, when building a wall, it’s important to make sure that the corners are squared off, which means that the angles between the walls should be right angles (90 degrees). If the angles are not right angles, the structure might be unstable.
Photography: In photography, the angle at which a photograph is taken can significantly impact the composition and overall feel of the image. Acute angles, which are angles that measure less than 90 degrees, can create a sense of tension or drama in a photograph, while obtuse angles, which are angles that measure more than 90 degrees but less than 180 degrees, can create a sense of calmness or tranquility.
Cooking: In cooking, it’s important to know the size of angles when preparing certain dishes. For example, when slicing vegetables for stir-fry, it’s often desirable to slice the vegetables at a slight angle in order to create longer, more visually appealing pieces.
The concept of classifying angles by size can be traced back to ancient civilizations, such as the Egyptians and the Greeks. These early cultures used basic geometry to solve problems related to construction, land surveying, and other practical matters. They also developed systems for measuring and classifying angles, using tools like a carpenter’s square or a plumb line.
Topics related to Classifying Angles by Size
Measuring angles: In order to classify angles by size, you need to know how to measure them. This involves using a tool called a protractor to determine the size of an angle in degrees.
Angle addition postulate: This is a mathematical principle that states that the measure of an angle formed by two rays with a common endpoint is equal to the sum of the measures of the two angles that the rays form. This principle can be used to solve problems involving the addition of angles.
Complementary angles: Complementary angles are pairs of angles whose measures add up to 90 degrees.
Supplementary angles: Supplementary angles are pairs of angles whose measures add up to 180 degrees.
Triangles: Triangles are three-sided polygons that are formed by three connected line segments. The sum of the interior angles of a triangle is always 180 degrees.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!