The angle addition postulate states that if we adjacent angles (share a common vertex and a common side), then the sum of those angles will be equal to the sum of the resulting angle.
Lesson
Notes
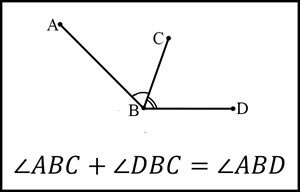
Practice Problems
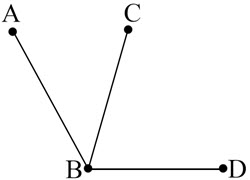
Use the above diagram to answer the following questions.
\(\textbf{1)}\) \(\text{m} \angle ABC= 32^{\circ}, \enspace \text{m} \angle CBD= 70^{\circ} \)
\(\textbf{2)}\) \(\text{m} \angle ABC= 38^{\circ}, \enspace \text{m} \angle CBD= 59^{\circ} \)
\(\textbf{3)}\) \(\text{m} \angle ABD= 112^{\circ}, \enspace \text{m} \angle CBD= 65^{\circ} \)
\(\textbf{4)}\) \(\text{m} \angle ABC= (2x+5)^{\circ}, \enspace \text{m} \angle CBD= (5x+10)^{\circ} \)
\(\textbf{5)}\) \(\text{m} \angle ABD= (10x+8)^{\circ}, \enspace \text{m} \angle ABC= (3x-2)^{\circ} \)

See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
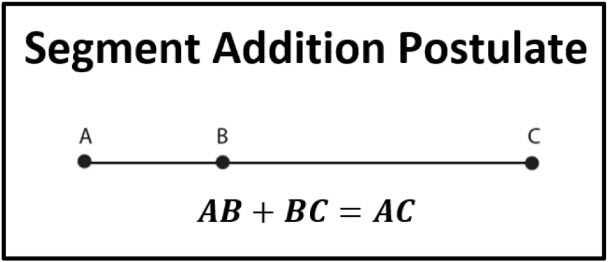
\(\bullet\text{ Segment Addition Postulate}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Complimentary and Supplementary Angles}\)
\(\,\,\,\,\,\,\,\,\)
In Summary
The Angle Addition Postulate states that if point B is in the interior of angle AOC, then the measure of angle AOB + the measure of angle BOC = the measure of angle AOC. This postulate is often used to find the measure of an angle when the measure of two other angles is known. It’s important to note that the Angle Addition Postulate only applies to angles in the same plane. If the angles are not in the same plane, the postulate does not hold.
The Angle Addition Postulate is typically introduced in an introductory geometry course, which is usually taken in high school. It is a basic concept in geometry and is often covered in the first few chapters of a geometry textbook. In this course, students learn about the properties of lines, angles, and shapes in two-dimensional space. They also learn about the relationships between these geometric objects, including the Angle Addition Postulate. In addition to the Angle Addition Postulate, students may also learn about other postulates and theorems related to angles, such as the Angle Bisector Theorem, the Exterior Angle Theorem, and the Inscribed Angle Theorem. These concepts build upon one another and are essential for understanding more advanced topics in geometry.
The Angle Addition Postulate, along with other basic concepts in geometry, has been known and used by mathematicians for thousands of years. Geometry, as a branch of mathematics, has a long and rich history that dates back to ancient civilizations. The ancient Egyptians, for example, used geometry in the construction of their pyramids, and the ancient Greeks developed many of the concepts and principles that form the foundation of modern geometry. Euclid, a Greek mathematician who lived around 300 BC, is often credited with codifying and organizing the principles of geometry in his famous work, “The Elements.” In this work, Euclid presented many of the basic principles and postulates of geometry, including the Angle Addition Postulate, as well as a number of theorems and proof techniques that are still used today.
Topics to Angle Addition Postulate
Triangle Sum Theorem: In a triangle, the measure of any angle is equal to the sum of the measures of the other two angles. This theorem is often used in conjunction with the Angle Addition Postulate to find the measure of an angle in a triangle.
Angle Bisector Theorem: The Angle Bisector Theorem states that if a line bisects an angle (divides it into two equal angles), then the line also bisects the side opposite the angle. This theorem can be used to find the length of a side in a triangle when the measures of two angles and one side are known.
Inscribed Angle Theorem: The Inscribed Angle Theorem states that if a line intersects two chords of a circle and the measure of the intercepted arc is greater than half the measure of the circle, then the measure of the inscribed angle is equal to half the measure of the intercepted arc.
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!