Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?

Notes

Practice Problems

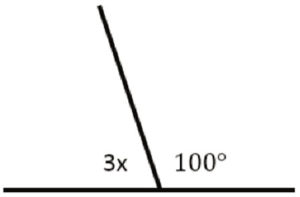
\(\textbf{1)}\) What is the value of x?

Show Answer

The answer is \(x= \displaystyle \frac{80}{3}^{\circ} \)

Show Work

\(\,\,\,\,\,\,3x+100=180\)

\(\,\,\,\,\,\,3x=80\)

\(\,\,\,\,\,\,x=\frac{80}{3}\)

The answer is \(x= \displaystyle \frac{80}{3}^{\circ} \)

\(\textbf{2)}\) An angle is \(30^{\circ}\) more than its compliment. What is the angle’s measure?

Show Answer

The answer is \(60^{\circ} \)

Show Work

\(\,\,\,\,\,\,(x)+(x-30)=90\)

\(\,\,\,\,\,\,2x-30=90\)

\(\,\,\,\,\,\,2x=120\)

\(\,\,\,\,\,\,x=60\)

\(\,\,\,\,\,\,\)The answer is \(60^{\circ} \)

\(\textbf{3)}\) An angle is \(10^{\circ}\) less than it’s supplement. What is the angle’s measure?

Show Answer

The answer is \(85^{\circ} \)

\(\textbf{4)}\) The supplement of an angle is triple the complement of the angle. What is the angle?

Show Answer

The answer is \(45^{\circ} \)

Show Work

\(\,\,\,\,\,\,\text{Supplement of an angle}=180-x\)

\(\,\,\,\,\,\,\text{Complement of an angle}=90-x\)

\(\,\,\,\,\,\,\left(180-x\right)=3\left(90-x\right)\)

\(\,\,\,\,\,\,180-x=270-3x\)

\(\,\,\,\,\,\,2x=90\)

\(\,\,\,\,\,\,x=45\)

The answer is \(45^{\circ} \)

See Related Pages\(\)

\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)

\(\bullet\text{ Angle Addition Postulate}\)
\(\,\,\,\,\,\,\,\,\)

In Summary

Complementary angles are two angles whose measures add up to 90 degrees. In other words, if one angle is x degrees, the other angle is 90-x degrees. Supplementary angles are two angles whose measures add up to 180 degrees. In other words, if one angle is x degrees, the other angle is 180-x degrees.
It’s important to note that complementary and suppplementary angles do not have to be adjacent (next to each other). However, it is common to see complementary and supplementary angles used in combination with adjacent angles (angles that share a vertex and side).

Complementary and supplementary angles are typically introduced in a high school geometry class or an introductory college-level math class. These concepts are important for understanding the properties of angles and for solving problems involving angles in geometry and trigonometry. Students may learn about complementary and supplementary angles as part of a unit on angles and angle relationships. This may include learning about the properties of angles, such as their measures and how they can be classified according to their size. Students may also learn how to use complementary and supplementary angles to solve problems involving angles in geometric figures.

The concept of complementary and supplementary angles has been known for thousands of years and has been studied by mathematicians and philosophers in many different cultures. The ancient Egyptians, for example, used a system of complementary and supplementary angles to measure the heights of pyramids and other structures.

About Andymath.com

Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.

Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.

Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!

Thank you for visiting. How exciting!