Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
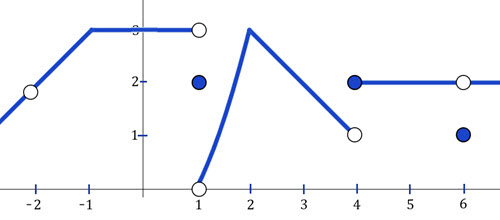
\(\textbf{1)}\) Is the graph continuous at \(x=-2\)?
\(\textbf{2)}\) Is the graph continuous at \(x=-1\)?
\(\textbf{3)}\) Is the graph continuous at \(x=0\)?
\(\textbf{4)}\) Is the graph continuous at \(x=1\)?

\(\textbf{5)}\) Is the graph continuous at \(x=2\)?
\(\textbf{6)}\) Is the graph continuous at \(x=3\)?
\(\textbf{7)}\) Is the graph continuous at \(x=4\)?
\(\textbf{8)}\) Is the graph continuous at \(x=5\)?
\(\textbf{9)}\) Is the graph continuous at \(x=6\)?
See Related Pages\(\)
\(\bullet\text{ Calculus Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Limits on Graphs}\)
\(\,\,\,\,\,\,\,\,\) \(…\)
\(…\)
\(\bullet\text{ Piecewise Functions- Limits and Continuity}\)
\(\,\,\,\,\,\,\,\,\)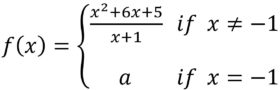 \(…\)
\(…\)
\(\bullet\text{ Infinite Limits}\)
\(\,\,\,\,\,\,\,\,\displaystyle \lim_{x\to 4^{+}} \frac{5}{x-4}\)
\(\bullet\text{ Limits at Infinity}\)
\(\,\,\,\,\,\,\,\,\displaystyle\lim_{x\to \infty}\frac{5x^2+2x-10}{3x^2+4x-5}\)
\(\bullet\text{ Trig Limits}\)
\(\,\,\,\,\,\,\,\,\displaystyle \lim_{\theta\to0} \frac{\sin \theta}{\theta}=1\)
In Summary
Continuity is a fundamental concept in calculus that deals with the smoothness and uninterrupted nature of functions. It involves understanding how a function’s output value changes as its input value changes. A function is said to be continuous at a particular point on its graph if the function’s value at that point is equal to its limit as the input value approaches that point. In other words, there should be no sudden jumps or breaks in the function’s output values as the input values change.
Continuity is typically introduced in calculus courses
One common mistake when working with continuity is to confuse it with other concepts, such as differentiability. It’s important to remember that a function can be continuous at a point even if it is not differentiable at that point.
The concept of continuity was first formally defined by the mathematician Bernard Bolzano in his work “The Paradoxes of the Infinite” in 1851. It was later refined and extended by other mathematicians, including Augustin-Louis Cauchy and Karl Weierstrass.
5 real world examples of Continuity
The temperature of a substance over time: As the temperature of a substance changes, we can plot its temperature on the y-axis and time on the x-axis. This graph will be a continuous curve, as the temperature of the substance will change smoothly and continuously over time.
The height of a ball as it bounces: When a ball bounces, its height will change continuously as it moves up and down. We can plot the height of the ball on the y-axis and time on the x-axis to create a continuous curve.
The volume of a gas in a container: As the pressure and temperature of a gas in a container change, the volume of the gas will also change. We can plot the volume of the gas on the y-axis and the pressure and temperature on the x-axis to create a continuous curve.
The velocity of a moving object: As an object moves, its velocity will change continuously as it accelerates or decelerates. We can plot the velocity of the object on the y-axis and time on the x-axis to create a continuous curve.
The concentration of a chemical in a solution: As a chemical is added to a solution, the concentration of the chemical in the solution will change. We can plot the concentration of the chemical on the y-axis and the amount of chemical added on the x-axis to create a continuous curve.
Math topics that use Continuity
Limits: In calculus, continuity is closely related to the concept of limits. A function is considered continuous at a point if the limit of the function at that point exists and is equal to the function’s value at that point.
Derivatives: Continuity is also an important concept when discussing the derivative of a function. A function is differentiable at a point if it is continuous at that point and the derivative exists at that point.
Integrals: Continuity is also a necessary condition for a function to be integrable. If a function is discontinuous at a point, the area under its graph may be difficult or impossible to determine, making it difficult or impossible to calculate the integral.
Taylor series: The Taylor series is a representation of a function as an infinite sum of terms that involve the function’s derivatives at a single point. In order for a Taylor series to converge to the original function, the function must be continuous.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!