Notes
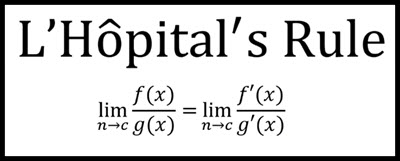
Questions
\(\textbf{1)}\) \( \displaystyle \lim_{x\to1} \displaystyle \frac{\ln{x}}{x-1} \)
\(\textbf{2)}\) \( \displaystyle \lim_{x\to\infty} \displaystyle \frac{lnx}{x} \)
\(\textbf{3)}\) \( \displaystyle \lim_{x\to\infty} xe^{-x} \)
\(\textbf{4)}\) \( \displaystyle \lim_{x\to0} (\sin x)^x \)
\(\textbf{5)}\) \( \displaystyle \lim_{x\to\infty} \displaystyle \frac{e^x}{x^3} \)
\(\textbf{6)}\) \( \displaystyle \lim_{x\to\infty} \displaystyle \frac{5x^2+2x-3}{4x^2-10x+7} \)
\(\textbf{7)}\) \( \displaystyle \lim_{x\to\infty} (1+ \frac{1}{x})^x \)
\(\textbf{8)}\) \( \displaystyle \lim _{x\to 0}\frac{\sin x}{x} \)
In Summary
L’Hôpital’s Rule is a method to evaluate limits that yield indeterminate forms. The process often changes an indeterminate form into an expression that can be easily evaluated with direct substitution. If it doesn’t work after the first application, you can repeat the process as many times as needed. It provides a way to find the value of a limit of a function when the limit cannot be computed using ordinary means.
The theorem states that if the limit of the quotient of two functions f(x) and g(x) as x approaches some value a is indeterminate (i.e., the value of the limit cannot be determined by direct substitution), then the limit of the quotient of the derivatives of f(x) and g(x) as x approaches a is equal to the original limit.
In order to apply L’Hôpital’s rule, the following conditions must be met:
\(\bullet\) The limit of the quotient of the two functions as x approaches a must be indeterminate.
\(\bullet\) The derivative of both functions must exist and be finite near the point a.
\(\bullet\) The derivative of the denominator must not be equal to 0 near the point a.
This is a very useful tool for solving problems in calculus.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!