Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Printable PDF and Answer Key 
Lesson
Practice Problems
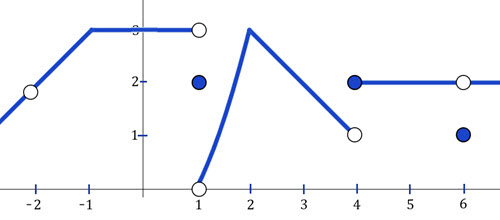
\(\textbf{1)}\)\( \displaystyle \lim_{x\to-2^{-}} f(x) \)
\(\textbf{2)}\)\( \displaystyle \lim_{x\to-2^{+}} f(x) \)
\(\textbf{3)}\)\( \displaystyle \lim_{x\to-2} f(x) \)
\(\textbf{4)}\) \(f(-2)\)

\(\textbf{5)}\)\( \displaystyle \lim_{x\to1^{-}} f(x) \)
\(\textbf{6)}\)\( \displaystyle \lim_{x\to1^{+}} f(x) \)
\(\textbf{7)}\) \( \displaystyle \lim_{x\to1} f(x) \)
\(\textbf{8)}\) \(f(1)\)

\(\textbf{9)}\)\( \displaystyle \lim_{x\to2^{-}} f(x) \)
\(\textbf{10)}\)\( \displaystyle \lim_{x\to2^{+}} f(x) \)
\(\textbf{11)}\) \( \displaystyle \lim_{x\to2} f(x) \)
\(\textbf{12)}\) \(f(2)\)

\(\textbf{13)}\)\( \displaystyle \lim_{x\to4^{-}} f(x) \)
\(\textbf{14)}\)\( \displaystyle \lim_{x\to4^{+}} f(x) \)
\(\textbf{15)}\) \( \displaystyle \lim_{x\to4} f(x) \)
\(\textbf{16)}\) \(f(4)\)

\(\textbf{17)}\)\( \displaystyle \lim_{x\to6^{-}} f(x) \)
\(\textbf{18)}\)\( \displaystyle \lim_{x\to6^{+}} f(x) \)
\(\textbf{19)}\) \( \displaystyle \lim_{x\to6} f(x) \)
\(\textbf{20)}\) \(f(6)\)
See Related Pages\(\)
\(\bullet\text{ Calculus Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Continuity on Graphs}\)
\(\,\,\,\,\,\,\,\,\) \(…\)
\(…\)
\(\bullet\text{ Piecewise Functions- Limits and Continuity}\)
\(\,\,\,\,\,\,\,\,\)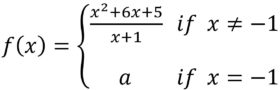 \(…\)
\(…\)
\(\bullet\text{ Infinite Limits}\)
\(\,\,\,\,\,\,\,\,\displaystyle \lim_{x\to 4^{+}} \frac{5}{x-4}\)
\(\bullet\text{ Limits at Infinity}\)
\(\,\,\,\,\,\,\,\,\displaystyle\lim_{x\to \infty}\frac{5x^2+2x-10}{3x^2+4x-5}\)
\(\bullet\text{ Trig Limits}\)
\(\,\,\,\,\,\,\,\,\displaystyle \lim_{\theta\to0} \frac{\sin \theta}{\theta}=1\)
In Summary
Limits are an important concept in calculus that allow us to understand how functions behave as they approach a certain point on a graph. Essentially, a limit tells us what a function’s value would be if it could reach that point, even if it doesn’t reach it.
To define limits on a graph, we need to consider a function’s behavior as it approaches a certain x-value from both the left and the right. If the function’s values on the left and right both approach the same y-value as x gets closer and closer to the limit, then we say the limit exists and is equal to that y-value. If the function’s values on the left and right do not approach the same y-value, then the limit does not exist.
Limits on graphs are typically introduced in a calculus course, usually at the beginning of the first semester. Limits are the foundation of calculus. Derivatives and Integrals both use limits. The modern definition of a limit was developed by Sir Isaac Newton and Gottfried Leibniz, two of the most influential figures in math.
It is important to note that continuity of a functions is defined using limits. A function is continuous at a point if the limit of the function as it approaches that point from both sides exists and is equal to the value of the function at that point.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!