Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Lesson
Questions & Answers
\(\textbf{1)}\)
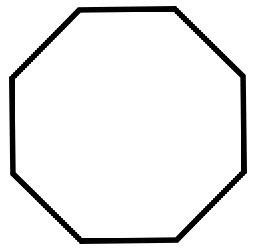
\(\textbf{2)}\)

\(\textbf{3)}\)
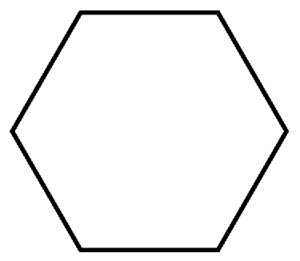
\(\textbf{4)}\)

\(\textbf{5)}\)
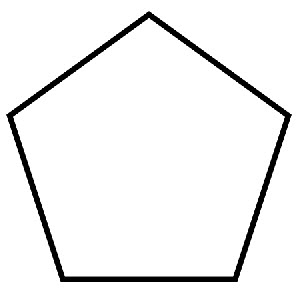
\(\textbf{6)}\)
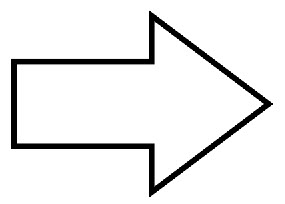
\(\textbf{7)}\)
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
In Summary
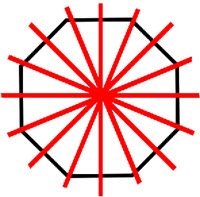
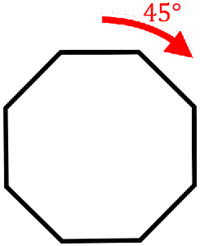
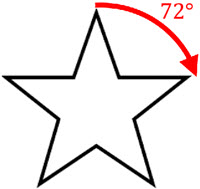
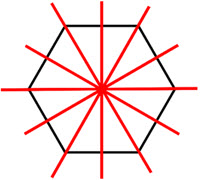
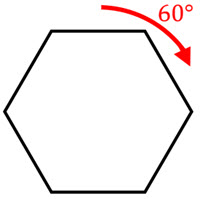
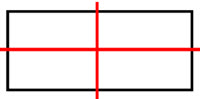
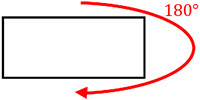
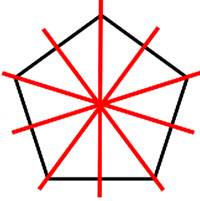
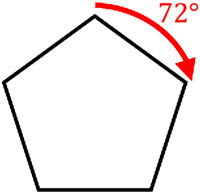
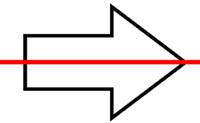
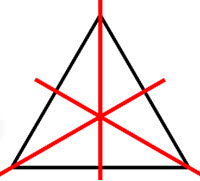
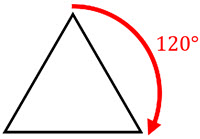
Line symmetry, also known as reflection symmetry, is a type of symmetry in which a figure is identical to its reflection across a line. Rotational symmetry, on the other hand, is a type of symmetry in which a figure is identical to its image after a certain number of rotations about a fixed point. Both line symmetry and rotational symmetry can be used to classify and analyze the symmetry of various shapes and patterns. In geometry, these symmetries are used to classify and study the properties of shapes and patterns, and they also play a role in other fields such as art, architecture, and biology.
Line symmetry and rotational symmetry are typically studied in geometry classes, which are usually taken in middle or high school. In a geometry class, students learn about the different types of symmetry, as well as other concepts such as points, lines, angles, and shapes.
One of the most common mistakes with line symmetry is choosing lines that bisect the area, like the diagonals of a non-square rectangle. While the diameters do cut the area in half, it is not a line of symmetry since it is not a mirror reflection to the other part of the rectangle.
Did you know that snowflakes have six-fold rotational symmetry? Snowflakes form when water vapor in the air condenses and freezes into ice crystals. The hexagonal shape of the ice crystals, which is made up of six identical sides, gives snowflakes their six-fold rotational symmetry. Snowflakes are a great example of the beauty and complexity that can arise from simple geometric principles. Their intricate and symmetrical patterns have long fascinated people, and they have been the subject of countless works of art and scientific study. In addition to snowflakes, there are many other natural and man-made objects that exhibit line symmetry or rotational symmetry. For example, many flowers, leaves, and seashells have bilateral symmetry, while many logos, patterns, and designs have rotational symmetry.
The concept of line symmetry can be traced back to the work of Euclid, a Greek mathematician who lived around 300 BC. Euclid wrote a treatise on geometry called “The Elements,” in which he defined and studied various types of symmetry, including line symmetry. The concept of rotational symmetry was also studied by the ancient Greeks, but it was not until the 1800s that it was studied in a more systematic way. The German mathematician August Ferdinand Möbius is credited with developing the concept of rotational symmetry in his work on topology, a branch of mathematics that studies the properties of shapes and spaces. Throughout history, many other mathematicians and scientists have contributed to the study of symmetry. These concepts continue to be an important part of mathematics and have numerous applications in a variety of fields.
Topics related to Line Symmetry and Rotational Symmetry
Geometry: Line symmetry and rotational symmetry are concepts that are studied in geometry, which is a branch of mathematics that deals with the study of shapes, sizes, and the properties of space. Other topics in geometry include points, lines, angles, and shapes such as circles, triangles, and quadrilaterals.
Symmetry groups: A symmetry group is a set of symmetries that can be applied to a figure or pattern. Line symmetry and rotational symmetry are types of symmetries that can be studied as part of a symmetry group.
Tessellations: A tessellation is a pattern of repeating shapes that fit together without any gaps or overlaps. Tessellations can be created using line symmetry and rotational symmetry, and they are often used in art and design.
Fractals: Fractals are complex patterns that are made up of repeating shapes and can be described using symmetry. Line symmetry and rotational symmetry can be used to analyze the symmetry of fractal patterns.
Group theory: Group theory is a branch of mathematics that deals with the study of symmetry groups and the ways in which they can be combined and transformed. Group theory is used to study symmetry in a variety of fields, including mathematics, physics, and chemistry.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!