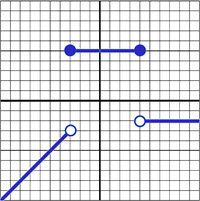
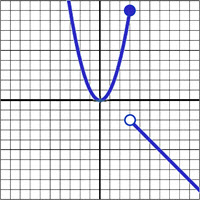
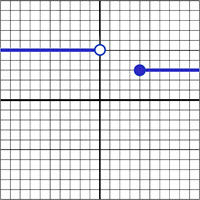
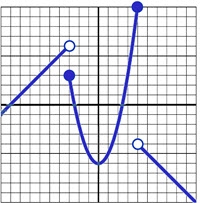
Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Graph the following piecewise functions.
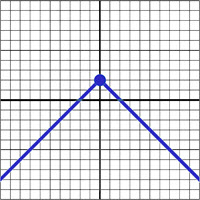
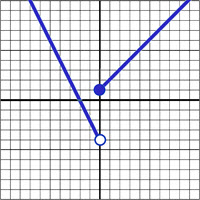
\(\textbf{1)}\) \(f(x) = \begin{cases}
x+2 & \text{if } x\lt 0 \\
-x+2 & \text{if }x\geq 0
\end{cases}\)
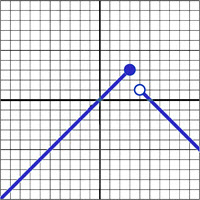
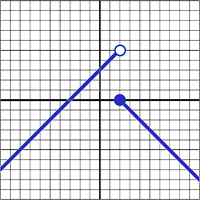
\(\textbf{2)}\) \(f(x) = \begin{cases}
x & \text{if } x\leq 3 \\
-x+5 & \text{if }x\gt 4
\end{cases}\)
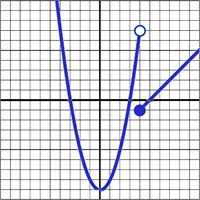
\(\textbf{3)}\) \(f(x) = \begin{cases}
x^2-9 & \text{if } x\lt 4 \\
x-5 & \text{if }x\geq 4
\end{cases}\)
\(\textbf{4)}\) \(f(x) = \begin{cases}
x & \text{if } x\lt 0 \\
-x+5 & \text{if }x\geq 0
\end{cases}\)
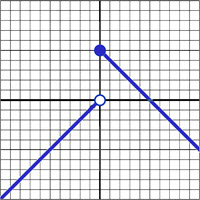
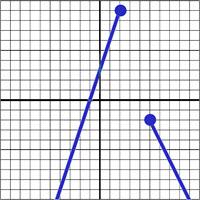
\(\textbf{5)}\) \(f(x) = \begin{cases}
-2x-4 & \text{if } x\lt 0 \\
x+1 & \text{if }x\geq 0
\end{cases}\)
\(\textbf{6)}\) \(f(x) = \begin{cases}
x+3 & \text{if } x\lt 2 \\
-x+2 & \text{if }x\geq 2
\end{cases}\)
\(\textbf{7)}\) \(f(x) = \begin{cases}
3x+3 & \text{if } x\leq 2 \\
-2x+8 & \text{if }x\geq 5
\end{cases}\)
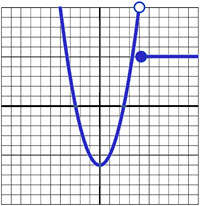
\(\textbf{8)}\) \(f(x) = \begin{cases}
x^2-6 & \text{if } x\lt 4 \\
5 & \text{if }x\geq 4
\end{cases}\)
\(\textbf{9)}\) \(f(x) = \begin{cases}
x & \text{if } x\lt -3 \\
5 & \text{if } -3\leq x\leq 4 \\
-2 & \text{if }x\gt 4
\end{cases}\)
\(\textbf{10)}\) \(f(x) = \begin{cases}
x^2 & \text{if } x\lt 3 \\
-x+1 & \text{if }x\geq 3
\end{cases}\)
\(\textbf{11)}\) \(f(x) = \begin{cases}
5 & \text{if } x\lt 0 \\
3 & \text{if }x\geq 4
\end{cases}\)
\(\textbf{12)}\) \(f(x) = \begin{cases}
x+9 & \text{if } x\lt -3 \\
x^2-6 & \text{if } -3\leq x\leq 4 \\
-x & \text{if }x\gt 4
\end{cases}\)
\(\textbf{13)}\) \(f(x) = \begin{cases}
x^2-8 & \text{if } x\lt 0 \\
5 & \text{if }x\geq 0
\end{cases}\)
\(\textbf{14)}\) \(f(x) = \begin{cases}
6 & \text{if } x\lt -4 \\
x+1 & \text{if } -4\leq x\lt 4 \\
-x+2 & \text{if }x\geq 4
\end{cases}\)
\(\textbf{15)}\) Graph the following piecewise function.
\(f(x) = \begin{cases}
x+2 & \text{if } x\geq 4 \\
x^2 & \text{if }x\lt 4
\end{cases}\)
Please see video for the graph

\(\textbf{16)}\) Identify the Domain and Range of the following piecewise function.
\(f(x) = \begin{cases}
-x+5 & \text{if } x\gt 4 \\
x & \text{if }x\leq 3
\end{cases}\)

\(\textbf{17)}\) Graph the following piecewise function.
\(f(x) = \begin{cases}
-x+5 & \text{if } x\gt 4 \\
x & \text{if }x\leq 3
\end{cases}\)
Please see video for the graph

\(\textbf{18)}\) Is the following continuous at \(x=4? \)
\(f(x) = \begin{cases}
-x+5 & \text{if } x\leq 4 \\
x-3 & \text{if } 4\lt x \lt 6 \\
x & \text{if }x\geq 6
\end{cases}\)

\(\textbf{19)}\) Is the following continuous at \( x=6? \)
\(f(x) = \begin{cases}
-x+5 & \text{if } x\leq 4 \\
x-3 & \text{if } 4\lt x \lt 6 \\
x & \text{if }x\geq 6
\end{cases}\)

\(\textbf{20)}\) Find the value of a that makes the function continuous.
\(f(x) = \begin{cases}
\frac{x^2+6x+5}{x+1} & \text{if } x \neq -1 \\
a & \text{if }x = -1
\end{cases}\)

\(\textbf{21)}\) Find the values of a and b that make the function continuous at all points.
\(f(x) = \begin{cases}
2x^2 & \text{if } x\leq 2 \\
ax+b & \text{if } 2\lt x \lt 4 \\
x^2+4 & \text{if }x\geq 4
\end{cases}\)

See Related Pages\(\)
\(\bullet\text{ Evaluating Piecewise Functions}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Absolute Value Functions as Piecewise Functions}\)
\(\,\,\,\,\,\,\,\,\)
In Summary
Graphing piecewise functions involves plotting a function that is defined by multiple pieces, each with its own function rule. These pieces are typically defined by x values within a certain range. Graphing piecewise functions is a useful tool for visualizing functions that have different behavior over different values of x. It allows us to see how the function changes as we move from one piece to another, which can be helpful in understanding the overall shape and behavior of the function.
Graphing piecewise functions is typically covered in a precalculus or calculus course. Some related topics to graphing piecewise functions include analyzing and interpreting functions, finding key features such as intercepts and asymptotes, and using functions to model real-world situations. Other related topics might include the study of continuous and discontinuous functions, or the use of piecewise functions in fields such as engineering and economics.
Real world examples of Graphing Piecewise Functions
A company might use a piecewise function to model the cost of producing a certain product as the number of units produced increases. The function might have different pieces for different ranges of production, with each piece representing a different cost structure. For example, the cost per unit might be lower for larger quantities due to economies of scale.
A piecewise function could be used to model the rate at which a substance dissolves in a solution. The function might have different pieces for different concentrations of the substance, with each piece representing a different rate of dissolution.
A piecewise function could be used to model the resistance of a material as a function of temperature. The function might have different pieces for different temperature ranges, with each piece representing a different resistance coefficient.
A piecewise function could be used to model the price of a commodity, such as oil, as a function of time. The function might have different pieces for different time periods, with each piece representing a different price trend.
A piecewise function could be used to model the speed of a vehicle as a function of time. The function might have different pieces for different time periods, with each piece representing a different speed.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!