Polygons are 2-dimensional shapes made of exclusively straight lines. If all the sides and angles are congruent, it is called a regular polygon.
Notes
Examples of Polygons
Not Polygons

| \(\underline{\text{Sides}}\) | \(\underline{\text{Name}}\) | \(\underline{\text{Example}}\) | \(\underline{\text{Sum of Interior Angles}}\) |
|---|---|---|---|
\(\textbf{Vocab}\)
Equilateral
An equilateral polygon has all sides of equal length.
Equiangular
An equiangular polygon has all interior angles equal.
Regular
A regular polygon is both equilateral (all sides are equal) and equiangular (all angles are equal).
Scalene
A scalene polygon has all sides and all angles of different lengths and measures, respectively.
Convex
A convex polygon has all its interior angles less than 180 degrees, and no sides are inwardly curved.
Concave
A concave polygon has at least one interior angle greater than 180 degrees, or at least one vertex pointing inward.
Diagonal
A diagonal is a line segment connecting two non-adjacent vertices of a polygon.
Exterior Angle
An exterior angle of a polygon is the angle formed between one side of the polygon and the extension of an adjacent side.
Interior Angle
An interior angle of a polygon is an angle formed between two adjacent sides inside the polygon.
Practice Problems
\(\textbf{1)}\) Is a circle a polygon?
\(\textbf{2)}\) What do you call a 12 sided convex polygon with equal length sides?
\(\textbf{3)}\) What does the word “regular” mean when describing polygons?
\(\textbf{4)}\) Are all squares polygons?
\(\textbf{5)}\) What is the specific name for regular quadrilaterals?
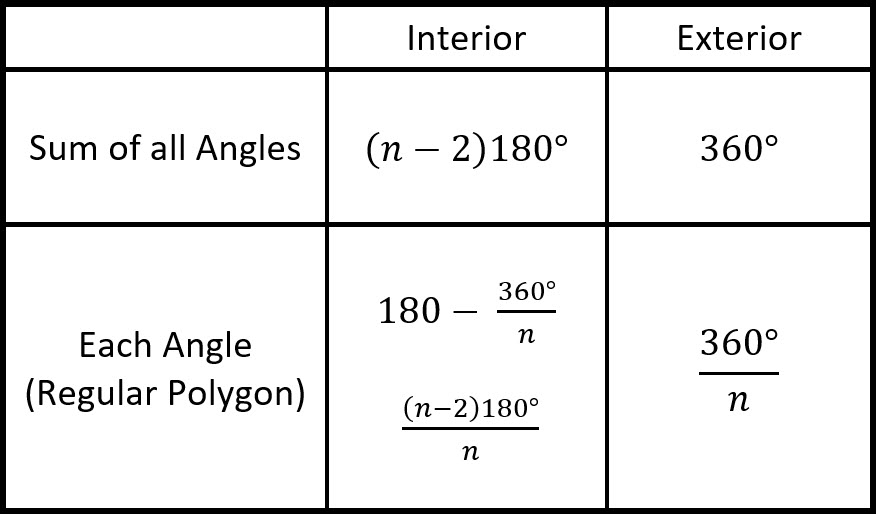
\(\textbf{6)}\) What is the sum of the interior angles of a pentagon?
\(\textbf{7)}\) What is the sum of the interior angles of a hexagon?
\(\textbf{8)}\) What is the sum of the interior angles of an octagon?
\(\textbf{9)}\) What is the sum of the exterior angles of a pentagon?
\(\textbf{10)}\) What is the sum of the exterior angles of a hexagon?
\(\textbf{11)}\) What is the sum of the exterior angles of an octagon?
\(\textbf{12)}\) How many degrees is each interior angle of a regular pentagon?
\(\textbf{13)}\) How many degrees is each interior angle of a regular hexagon?
\(\textbf{14)}\) How many degrees is each interior angle of a regular octagon?
\(\textbf{15)}\) If a regular polygon has an exterior angle equal to \(20^{\circ}\), how many sides does the polygon have?
\(\textbf{16)}\) A regular polygon has interior angles equal to \(120^{\circ}\), name the polygon.
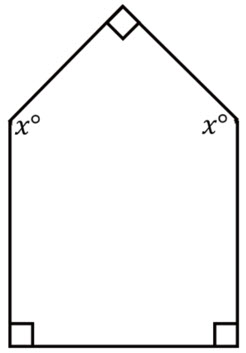
\(\textbf{17)}\) Solve for x.
True or False
\(\textbf{18)}\) The sum of the exterior angles of a triangle is the same as a square.
\(\textbf{19)}\) The sum of the interior angles and the sum of the exterior angles of a quadrilateral are always the same.
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Angles of Polygons}\)
\(\,\,\,\,\,\,\,\,\text{Sum}=(n-2)180^{\circ}…\)
\(\bullet\text{ Area of a Regular Polygon (Apothem)}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\frac{1}{2}\text{(Apothem)(Perimeter)}\)…
\(\bullet\text{ Population Density}\)
\(\,\,\,\,\,\,\,\,\text{Population Density}=\displaystyle\frac{\text{Number of People}}{\text{Area}}\)…
\(\bullet\text{ Andymath Homepage}\)
In Summary
Polygons are two-dimensional shapes with straight sides and angles. They can have anywhere from three sides (a triangle) to any nnumber of finite sides. The specific name of a polygon depends on the number of sides it has. Triangles (3 sides), quadrilaterals (4 sides), and pentagons (5 sides) are all examples of polygons.
Polygons are typically covered in geometry classes, which are typically taken in high school. However, the basic concepts of polygons may also be introduced in earlier math classes, such as in middle school. Understanding polygons allows us to understand and analyze the properties of shapes and their relationships to each other. Polygons also have practical applications in real-life situations, such as in construction and design.
A regular polygon is a polygon with sides of equal length and angles of equal measure. An irregular polygon is a polygon with sides of different lengths and/or angles of different measures.
Polygons have been studied for centuries, with some of the earliest known references to them dating back to ancient Greek mathematics. There are many related topics to polygons that are also studied in geometry, such as lines, angles, and triangles. Other related topics include circles, 3-dimensional shapes, and geometric transformations such as rotations and translations. Understanding these concepts can help us better understand and analyze the properties of polygons.
Real world examples of polygons
A stop sign is an octagon, which is a polygon with eight sides.
Many parts of houses can be thought of as polygons. The walls of the house form the sides of the polygon, and the corners where the walls meet form the angles.
A soccer field is a rectangle, which is a polygon with four sides and four right angles.
A hexagonal honeycomb is a polygon with six sides. Bees use hexagons to build their honeycombs because it is an efficient shape for using a small amount of wax to enclose a large amount of honey.
Topics that use polygons
Trigonometry: Trigonometry is the study of triangles and their properties, and polygons are often used to represent triangles in trigonometry. Trigonometry is used to calculate angles and distances, and is often used in fields such as engineering and navigation.
Geometry: As mentioned earlier, geometry is the study of shapes and their properties, and polygons are a fundamental concept in geometry. In geometry, we learn about the properties of different polygons, such as the number of sides, the length of the sides, and the measure of the angles.
Graph theory: Graph theory is the study of graphs, which are used to represent relationships between objects. Polygons can be used to represent nodes in a graph, and the sides of the polygon represent the relationships between the nodes.
Computer graphics: Polygons are used extensively in computer graphics to create 3-dimensional shapes and objects. When creating 3D models, polygons are used to define the shape and surface of the object.
Tessellations: A tessellation is a pattern of shapes that fit together perfectly without any gaps. Polygons are often used to create tessellations because they can be arranged in a variety of patterns to form a complete, seamless pattern.
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!