Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Notes
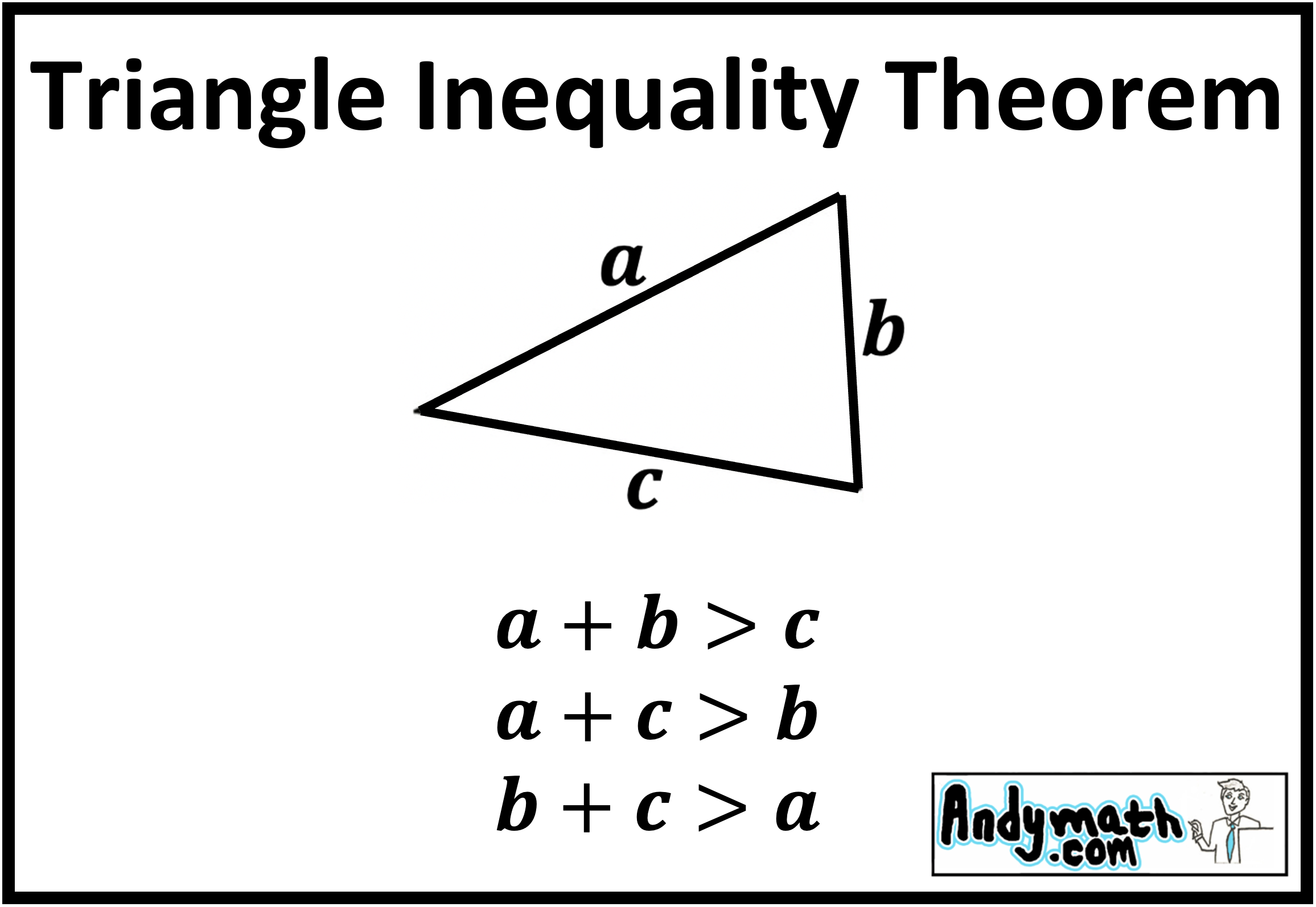
Problems
\(\textbf{1)}\) Can a triangle have side lengths 3, 5 and 7?
\(\textbf{2)}\) Can a triangle have side lengths 4, 5 and 9?
\(\textbf{3)}\) A triangle has side lengths 5 feet and 7 feet. What is the range of possible lengths for the third side?
\(\textbf{4)}\) A triangle has side lengths 4 feet and 10 feet. What is the range of possible lengths for the third side?
\(\textbf{5)}\) If a triangle has lengths 10 and 20, What is the range of possible lengths for the third side?
\(\textbf{6)}\) A triangle has one side length \(x\) and another side length \(5x\). What is the range of possible lengths for the third side \(s\)?
\(\textbf{7)}\) If \(AC = AB,\) and the length of \(AB\) is an integer, what is the smallest possible value of \(AB\)?
Challenge Problem
\(\textbf{8)}\) A triangle has whole number sides. The perimeter is \(30\). If one side is \(10\), what is the shortest possible distance another side could be?
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
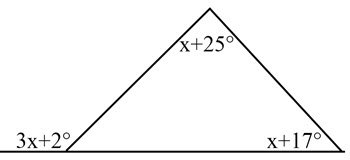
\(\bullet\text{ Exterior Angle Theorem}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Triangle Angle Sum Theorem}\)
\(\,\,\,\,\,\,\,\,\angle A+ \angle B+ \angle C=180^{\circ}…\)
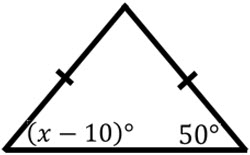
\(\bullet\text{ Isosceles Triangles}\)
\(\,\,\,\,\,\,\,\,\)
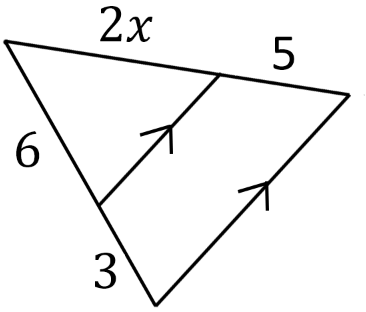
\(\bullet\text{ Side Splitter Theorem}\)
\(\,\,\,\,\,\,\,\,\)
In Summary
The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. In short, the longest side can’t be longer than the sum of the two shorter sides. This makes intuitive sense. If the third side was longer then the sum of the other two sides, then the triangle wouldn’t be able to close. For example if a triangle had side lengths 2,3 and 9. The sides of length 2 and 3 wouldn’t be able to connect because the side length of 9 is too long.
The Triangle Inequality Theorem is a fundamental concept in geometry. It is used many proofs involving triangles. And is frequently used in problemes involvoing specific triangles to show the range of possible values.
The Triangle Inequality Theorem is first taught in middle school math or high school geometry courses. It also shows up in trigonometry and other topics that involve triangles.
The most common mistake with Triangle Inequality Theorem is mistaking it for \(a+b \ge c \), when in fact it is \(a+b \gt c\). The third side must be greater than the sum of the two smaller sides, it can not be equal. If it were equal the triangle would be a flat line with no area.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!