When 2 lines cross, 4 angles are formed. The angles opposite of each other are called vertical angles and they are congruent (have the same angle measure.)
Practice Problems
\(\textbf{1)}\) Solve for x.
![Link to Youtube Video Solving Question Number 1](https://andymath.com/wp-content/uploads/2020/08/play-video.jpg")
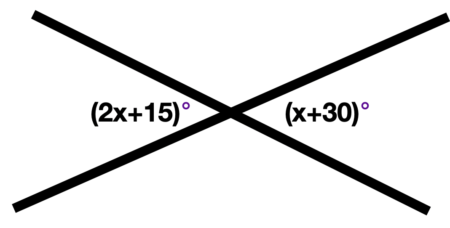
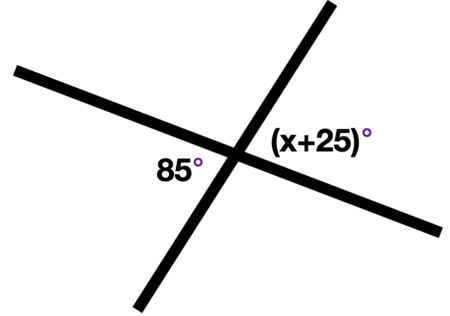
\(\textbf{2)}\) Solve for x.
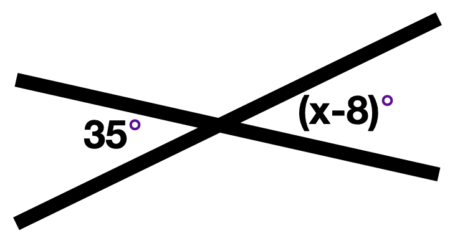
\(\textbf{3)}\) Solve for x.
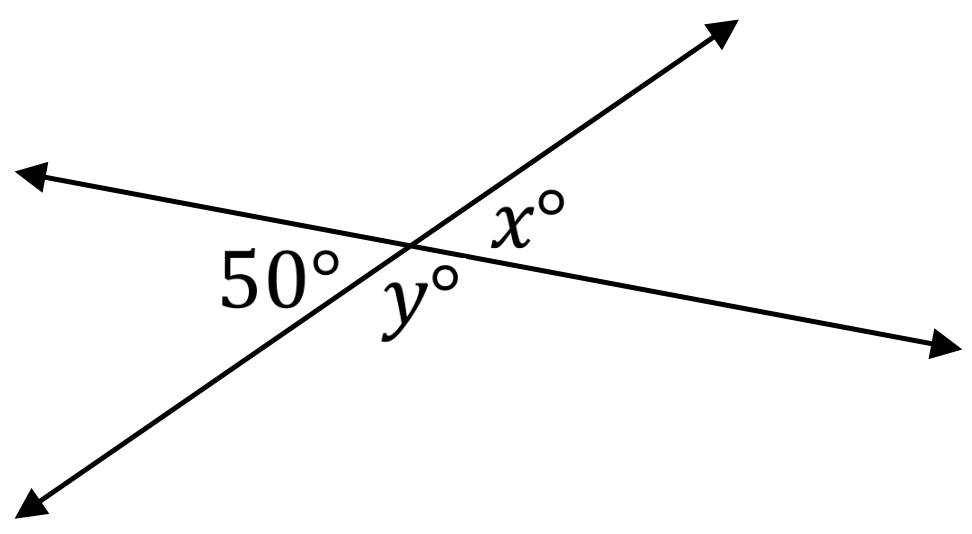
\(\textbf{4)}\) Solve for x and y.
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Angle Addition Postulate}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Complimentary and Supplementary Angles}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Andymath Homepage}\)
In Summary
Vertical angles are a pair of angles that are opposite each other and are formed by two intersecting lines. Vertical angles are always congruent, which means that they have the same measure.
Vertical angles are typically covered in a geometry course. These topics are usually introduced in middle school or high school math classes, although they can also be covered in lower-level college math courses. In geometry, students learn about the properties and characteristics of angles.
Real world examples of Vertical Angles
Architecture: In architecture, it’s important to consider the angles of various structures in order to ensure that they are stable and aesthetically pleasing. For example, when designing a building, architects might use vertical angles to create a sense of balance and symmetry in the design.
Photography: In photography, the angle at which a photograph is taken can significantly impact the composition and overall feel of the image. By using vertical angles, photographers can create a sense of depth and perspective in their images.
Art: In art, vertical angles can be used to create a sense of movement or dynamism in a piece. For example, an artist might use vertical angles to create the illusion of a figure in motion or to depict the lines of a landscape in a more dynamic way.
Topics related to Vertical Angles
Congruent angles: As mentioned earlier, vertical angles are always congruent, which means that they have the same measure. This concept is closely related to vertical angles and is important to understand when working with these types of angles.
Parallel lines: Parallel lines are lines that are always the same distance apart and never intersect. When two lines are parallel, the angles formed by those lines are also related. Specifically, corresponding angles, which are pairs of angles that lie on the same side of the transversal (a line that intersects the two parallel lines), are congruent.
Transversals: A transversal is a line that intersects two or more lines at different points. When a transversal intersects two lines, it creates a series of angles that are related in specific ways. These relationships, known as angle pair relationships, include corresponding angles, alternate interior angles, and alternate exterior angles.
Angle addition postulate: The angle addition postulate is a mathematical principle that states that the measure of an angle formed by two rays with a common endpoint is equal to the sum of the measures of the two angles that the rays form. This principle can be used to solve problems involving the addition of angles.
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!