Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Lessons
Notes
Questions & Answers
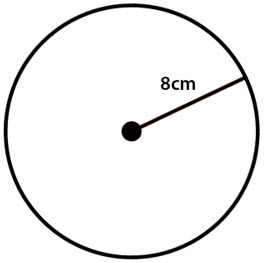
\(\textbf{1)}\) What is the area of the circle?
\(\textbf{2)}\) What is the circumference of the circle?
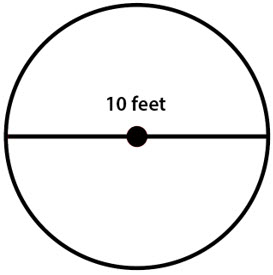
\(\textbf{3)}\) What is the area of the circle?
\(\textbf{4)}\) What is the circumference of the circle?
\(\textbf{5)}\) The area of a circle is \(250\) meters squared. What is the radius?
\(\textbf{6)}\) The circumference of a circle is \(20\pi\) feet. What is the diameter?
Challenge Problems
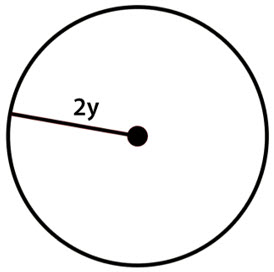
\(\textbf{7)}\) Express the area of the circle in terms of \(y\) and \(\pi\).
\(\textbf{8)}\) Find the circumference of the circle in terms of \(y\) and \(\pi\).
\(\textbf{9)}\) Express the area of the above circle in terms of \(x\) and \(\pi\).
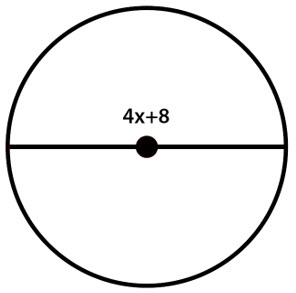
\(\textbf{10)}\) Express the circumference of the above circle in terms of \(x\) and \(\pi\).
Standardized Test Practice
\(\textbf{11)}\) The circumference of a circle is \(12 \pi \). What is the area of the circle?
\(\,\,\,\,\,\,\) a. \(12 \pi\)
\(\,\,\,\,\,\,\) b. \(24 \pi\)
\(\,\,\,\,\,\,\) c. \(36 \pi\)
\(\,\,\,\,\,\,\) d. \(6 \pi\)
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Area and Perimeter of Rectangles}\)
\(\,\,\,\,\,\,\,\,\)
\(\,\, A=bh, \,\, P=2b+2h…\)
\(\bullet\text{ Area and Perimeter of Triangles}\)
\(\,\,\,\,\,\,\,\,\)
\(\,\, A=\frac{1}{2}bh, \,\, P=s_1+s_2+s_3…\)
\(\bullet\text{ Area and Circumference of Circles}\)
\(\,\,\,\,\,\,\,\,\)
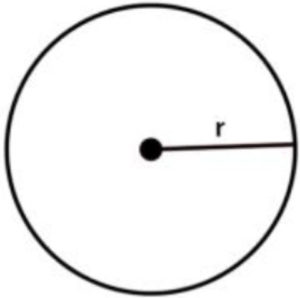\(\,\, A= \pi r^2, \,\,C=2 \pi r…\)
\(\bullet\text{ Area of Trapezoids}\)
\(\,\,\,\,\,\,\,\,\)
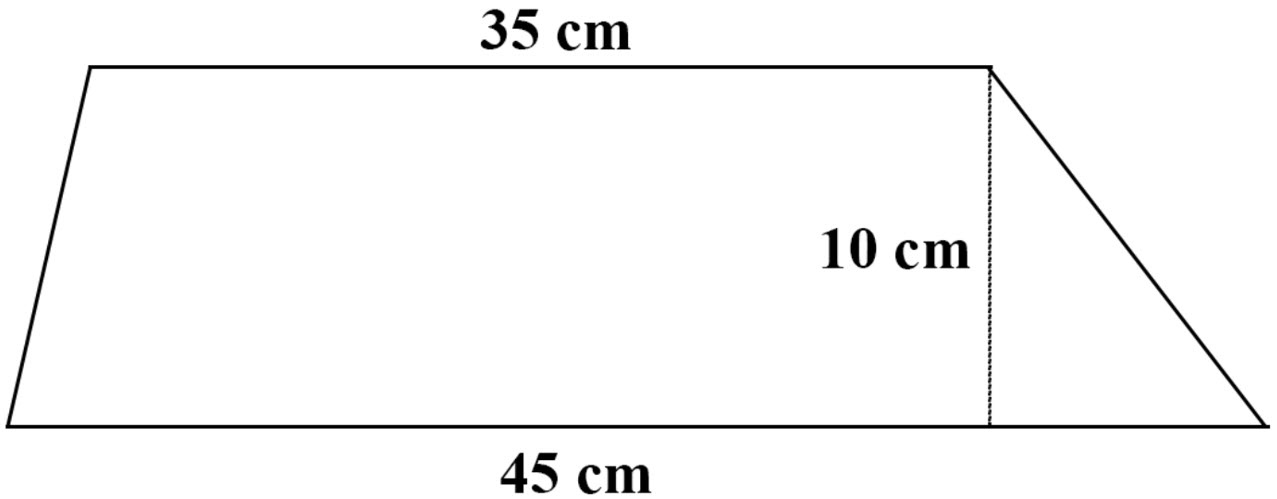\(A=\frac{1}{2}(b_1+b_2)\cdot h…\)
In Summary
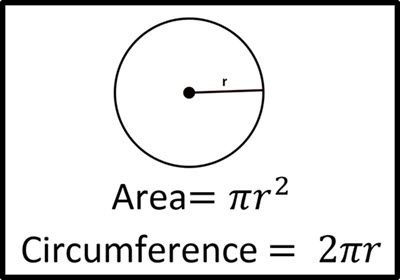
The area of a circle is the measure of the region enclosed by the circle. It is denoted by A and is given by the formula: \(A = πr^2\)
where r is the radius of the circle.
The circumference of a circle is the distance around the circle. It is denoted by C and is given by the formula:
\(C = 2πr\)where r is the radius of the circle.
It’s important to note that these formulas apply to all circles, no matter their size or shape.
The concepts of area and circumference of a circle are typically introduced in a high school geometry class. These concepts are also a part of algebra 2 and pre-calculus courses. In college, these concepts may be covered in courses such as calculus or engineering.
A common mistake students make when first working with areas and circumference of circles is confusing the radius and diameter of a circle: The radius is the distance from the center of the circle to any point on the circle, while the diameter is the distance across the circle through the center.
Did you know that the ratio of the circumference of a circle to its diameter is always the same, no matter the size of the circle? This constant ratio is equal to pi (π), which is approximately equal to 3.14. This means that if you divide the circumference of a circle by its diameter, you will always get the same value, which is pi.
Real world examples of Area and Circumference of Circles
Engineering: Engineers use the area and circumference of circles to design circular objects such as gears, wheels, and pulleys. These objects are often used in machines and structures, and the size and shape of the circles must be carefully calculated to ensure that they function properly.
Construction: The area and circumference of circles are important in construction, as they are used to calculate the amount of material needed for circular objects such as pipes, tanks, and concrete slabs.
Landscaping: Landscapers use the area and circumference of circles to design circular gardens and patios. They may also use these concepts to calculate the amount of grass seed or mulch needed to cover circular areas.
Medicine: In medicine, the area and circumference of circles are used to measure the size of organs and other body parts. For example, doctors may use these concepts to determine the size of a person’s head or the size of a tumor.
Cooking: The area and circumference of circles are also used in cooking. For example, bakers may use these concepts to determine the amount of dough needed to make a circular pie crust or to calculate the size of a circular cake pan.
The concept of the area and circumference of a circle can be traced back to ancient civilizations, such as the ancient Egyptians and Greeks. These early cultures used geometric principles to solve practical problems, such as how to measure land or design structures. One of the earliest known definitions of the circumference of a circle is attributed to the ancient Greek mathematician and philosopher Archimedes. In his work “The Measurement of a Circle,” Archimedes derived a formula for the circumference of a circle using a method known as exhaustion. This method involves approximating the value of a quantity by using a series of increasingly accurate estimations.
The modern symbol for pi (π) was first used by the Welsh mathematician William Jones in 1706. Jones used the symbol in a book called “Synopsis Palmariorum Matheseos,” which introduced the concept of pi as the ratio of the circumference of a circle to its diameter.
Topics related to Area and Circumference of Circles
Radius and diameter: The radius and diameter of a circle are important concepts that are related to the area and circumference of a circle. The radius is the distance from the center of the circle to any point on the circle, while the diameter is the distance across the circle through the center. The radius and diameter are used in the formulas for the area and circumference of a circle.
Pi (π): Pi (π) is an irrational number that is approximately equal to 3.14. It is used in the formulas for the area and circumference of a circle and is defined as the ratio of the circumference of a circle to its diameter.
Geometry: Geometry is a branch of mathematics that deals with the study of shapes, sizes, and the properties of space. It is a foundational subject that is important for many fields, including engineering, architecture, and computer science. The area and circumference of a circle are important concepts in geometry.
Trigonometry: Trigonometry is a branch of mathematics that deals with the study of triangles and the relationships between their sides and angles. It is used in a wide range of fields, including engineering, physics, and astronomy.
Calculus: Calculus is a branch of mathematics that deals with the study of rates of change and the accumulation of quantities. It is used in a wide range of fields, including physics, engineering, and economics. The area and circumference of a circle are important concepts in calculus, as they are used to understand the behavior of functions and to solve problems involving geometric figures.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!