Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Notes
Questions
\(\textbf{1)}\) What is the area of the triangle below?
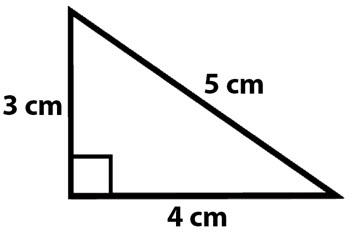
\(\textbf{2)}\) What is the perimeter of the triangle below?
\(\textbf{3)}\) What is the area of the triangle below?
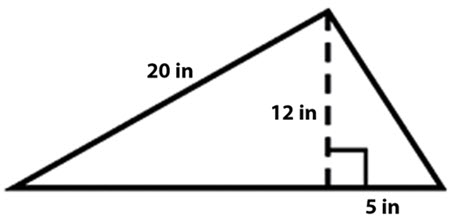
\(\textbf{4)}\) What is the perimeter of the triangle below?
\(\textbf{5)}\) What is the area of the triangle below?
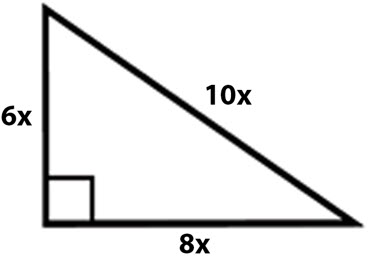
\(\textbf{6)}\) What is the perimeter of the triangle below?
\(\textbf{7)}\) The area of a triangle is \(30 \) cm\(^2\). If the base is \(3\) cm, what is the height?
\(\textbf{8)}\) What is the area of a triangle with base \(4 \frac{1}{2} \) ft and height \(3 \frac{1}{4}\) ft?
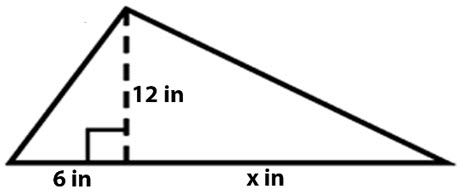
\(\textbf{9)}\) The area of the below triangle is \(96\) in\(^2\). What is the value of x?
Challenge Problems
\(\textbf{10)}\) What is the area of a triangle with vertices at \((2{,}3), (2{,}8) \) and \((8{,}7) \) ft?
\(\textbf{11)}\) What is the area of a triangle with vertices at \((5{,}9), (9{,}9) \) and \((4{,}4) \) ft?
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Area and Perimeter of Rectangles}\)
\(\,\,\,\,\,\,\,\,\)
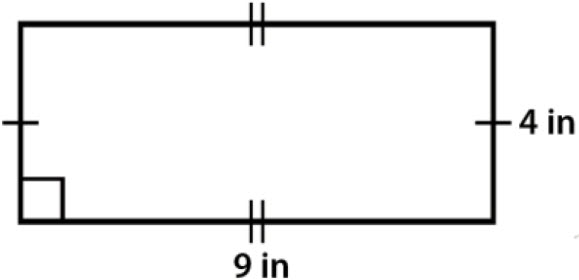\(\,\, A=bh, \,\, P=2b+2h…\)
\(\bullet\text{ Area and Circumference of Circles}\)
\(\,\,\,\,\,\,\,\,\)
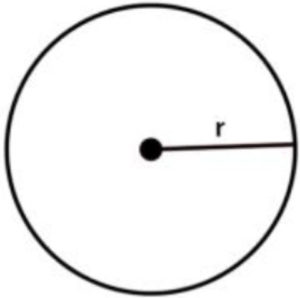\(\,\, A= \pi r^2, \,\,C=2 \pi r…\)
\(\bullet\text{ Area of Trapezoids}\)
\(\,\,\,\,\,\,\,\,\)
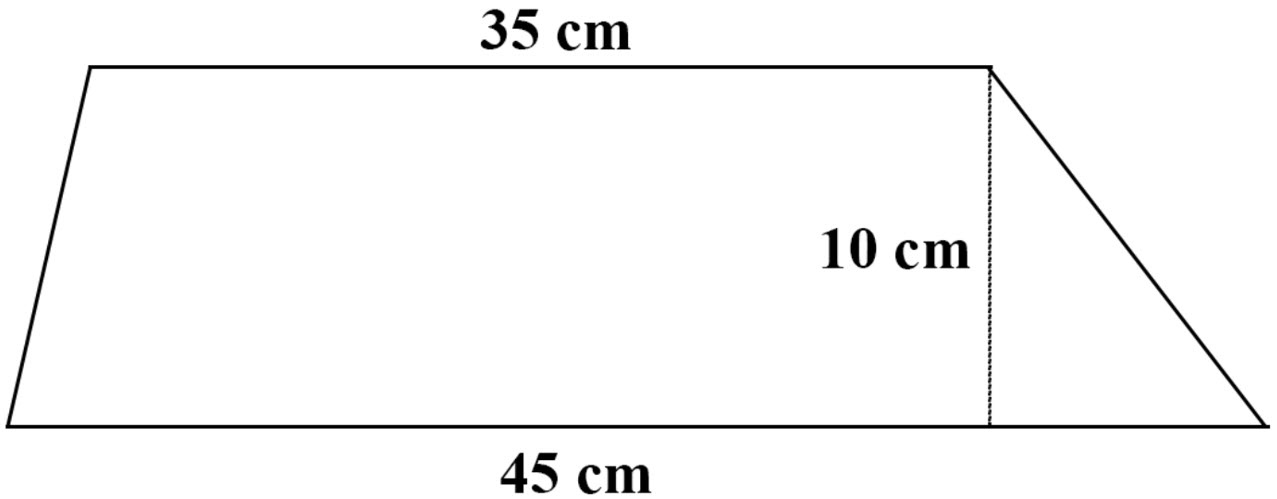\(A=\frac{1}{2}(b_1+b_2)\cdot h…\)
\(\bullet\text{ Area of Compound Figures}\)
\(\,\,\,\,\,\,\,\,\)
\(\)
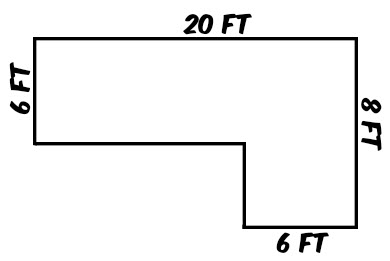In Summary
The area of a triangle is a measure of the size of the triangle. It is calculated by multiplying the base of the triangle by the height of the triangle, and then dividing the result by 2. The base of the triangle is any side of the triangle, and the height of the triangle is a line drawn from the base to the opposite vertex (corner) that is perpendicular to the base.
The perimeter of a triangle is the distance around the outside of the triangle. It is calculated by adding up the lengths of all three sides of the triangle.
The topic of finding the area and perimeter of triangles is typically covered in a middle school or high school math class, such as geometry. In geometry, students learn about different types of two-dimensional shapes, including triangles, and how to measure and calculate their characteristics, such as area and perimeter.
Real world examples of Area and Perimeter of Triangles
Construction: In construction, triangles are often used in the design of buildings and other structures. For example, a triangle may be used as a support beam to distribute weight evenly across a structure. In these cases, the area and perimeter of the triangle may be used to calculate the amount of material needed to construct the beam and to ensure that the beam is strong enough to support the load.
Landscaping: In landscaping, triangles may be used to create geometric patterns or to divide a space into smaller sections. For example, a triangle may be used to create a flower bed in a garden. The area of the triangle can be used to calculate how much soil and plants are needed to fill the bed.
Cooking: In cooking, triangles are often used to divide a pizza or other type of pie into equal slices. The area of the triangle can be used to calculate how much food is in each slice.
Sports: In sports, triangles are often used to create strategic positions on the field or court. For example, in soccer, players may form a triangle shape to pass the ball around and keep possession of it. The perimeter of the triangle can be used to calculate the distance covered by the players as they move the ball.
Navigation: In navigation, triangles are often used to triangulate a position. By measuring the angles and distances between three known points, a navigator can determine their own position. The perimeter of the triangle can be used to calculate the distances between the points.
The concept of area and perimeter has been known for thousands of years, and it is likely that different civilizations and cultures independently discovered these concepts and developed methods for calculating them. The ancient Egyptians, for example, were skilled mathematicians who were able to calculate the area of triangles and other geometric shapes using geometrical methods. The ancient Greeks, including Euclid and Archimedes, also made significant contributions to the study of geometry and developed many of the concepts and principles that are still used today.
Topics related to Area and Perimeter of Triangles
Geometry: Geometry is the branch of mathematics that deals with the properties and relationships of points, lines, angles, surfaces, and solids. It is a fundamental mathematical subject that is closely related to area and perimeter, as these concepts are used to measure and calculate the characteristics of geometric shapes.
Trigonometry: Trigonometry is the branch of mathematics that deals with the relationships between the sides and angles of triangles. It is often used in conjunction with geometry to solve problems involving triangles, including problems involving the area and perimeter of triangles.
Similar triangles: Similar triangles are triangles that have the same shape but may be different sizes. The ratio of the sides of similar triangles is always the same, which means that if you know the ratio of the sides of one similar triangle, you can use it to find the sides of another similar triangle. This can be useful in solving problems involving the area and perimeter of triangles.
Pythagorean theorem: The Pythagorean theorem is a fundamental mathematical principle that states that in a right triangle (a triangle with one 90-degree angle), the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem can be used to solve problems involving triangles, including problems involving the area and perimeter of triangles.
Triangles in the coordinate plane: Triangles can also be represented and studied in the coordinate plane, which is a two-dimensional grid used to represent points in space. The coordinates of the vertices of a triangle can be used to find the length of its sides and to calculate its area and perimeter.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!