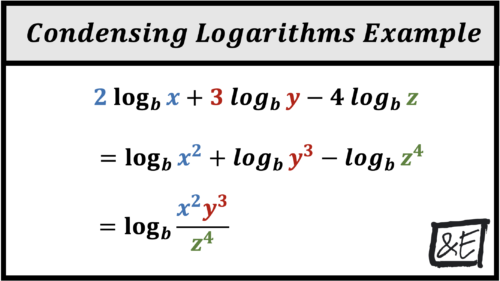Why do we use logarithms?

Logarithms were invented to deal with this type of problem.

\(3^x=25\).

How would we solve this for x? We could guess and check multiple times or we could create a method to solve it. Logarithms are that method.

Definition of Logarithms

A logarithm can be defined this way.

Logarithmic Form & Exponential Form

\(\displaystyle \log_{b}m=x \,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,\, b^{x}=m\)

So we can take our original \(3^x=25\) and rewrite it as \(\log_{3}25=x\).

Would you like to practice some?

\(\textbf{1)}\) Write \(\log_{b}\frac{1}{5}=25\) in exponential form.

Show Answer

The answer is \( b^{25}=\frac{1}{5} \)

\(\textbf{2)}\) Write \(\log_{4}x=2\) in exponential form.

Show Answer

The answer is \( 4^{2}=x \)

\(\textbf{3)}\) Write \(\log_{b}25=2\) in exponential form.

Show Answer

The answer is \( b^{2}=25 \)

\(\textbf{4)}\) Write \(\log_{3}9=x\) in exponential form.

Show Answer

The answer is \( 3^{x}=9 \)

\(\textbf{5)}\) Write \(m^5=32\) in logarithmic form.

Show Answer

The answer is \( \log_{m}32=5 \)

\(\textbf{6)}\) Write \(3^x=27\) in logarithmic form.

Show Answer

The answer is \( \log_{3}27=x \)

\(\textbf{7)}\) Write \(2^4=x\) in logarithmic form.

Show Answer

The answer is \( \log_{2}x=4 \)

\(\textbf{8)}\) Write \(x^{10}=100\) in logarithmic form.

Show Answer

The answer is \( \log_{x}100=10 \)

Evaluating Logarithms

Evaluating logarithms is one of the funnest things to do with logarithms.

For example, if you have

\(log_2{8}\),

you can set it equal to x

\(log_2{8}=x\),

then rewrite it in exponential form as

\(2^x=8\),

then rewrite it as

\(2^x=2^3\),

then you know

\(x=3\).

Would you like to practice some?

\(\textbf{9)}\) \(\log_{3}9\)

Show Answer

The answer is \(2\)

Show Work

\(\,\,\,\,\,\log_{3}9=x\)

\(\,\,\,\,\,3^x=9\)

\(\,\,\,\,\,3^x=3^{2}\)

\(\,\,\,\,\,x=2\)

\(\textbf{10)}\) \(\log_{3}3\)

Show Answer

The answer is \(1\)

Show Work

\(\,\,\,\,\,\log_{3}3=x\)

\(\,\,\,\,\,3^x=3\)

\(\,\,\,\,\,3^x=3^{1}\)

\(\,\,\,\,\,x=1\)

\(\textbf{11)}\) \(\log_{2}8\)

Show Answer

The answer is \(3\)

Show Work

\(\,\,\,\,\,\log_{2}8=x\)

\(\,\,\,\,\,2^x=8\)

\(\,\,\,\,\,2^x=2^{3}\)

\(\,\,\,\,\,x=3\)

\(\textbf{12)}\) \(\log_{4}16\)

Show Answer

The answer is \(2\)

Show Work

\(\,\,\,\,\,\log_{4}16=x\)

\(\,\,\,\,\,4^x=16\)

\(\,\,\,\,\,4^x=4^2\)

\(\,\,\,\,\,x=2\)

\(\textbf{13)}\) \(\log_{6}6\)

Show Answer

The answer is \(1\)

Show Work

\(\,\,\,\,\,\log_{6}6=x\)

\(\,\,\,\,\,6^x=6\)

\(\,\,\,\,\,6^x=6^1\)

\(\,\,\,\,\,x=1\)

\(\textbf{14)}\) \(\log_{2}32\)

Show Answer

The answer is \(5\)

Show Work

\(\,\,\,\,\,\log_{2}32=x\)

\(\,\,\,\,\,2^x=32\)

\(\,\,\,\,\,2^x=2^5\)

\(\,\,\,\,\,x=5\)

\(\textbf{15)}\) \(\log_{6}1\)

Show Answer

The answer is \(0\)

Show Work

\(\,\,\,\,\,\log_{6}1=x\)

\(\,\,\,\,\,6^x=1\)

\(\,\,\,\,\,6^x=6^0\)

\(\,\,\,\,\,x=0\)

\(\textbf{16)}\) \(\log_{2}\frac{1}{2}\)

Show Answer

The answer is \(-1\)

Show Work

\(\,\,\,\,\,\log_{2}\frac{1}{2}=x\)

\(\,\,\,\,\,2^x=\frac{1}{2}\)

\(\,\,\,\,\,2^x=2^{-1}\)

\(\,\,\,\,\,x=-1\)

\(\textbf{17)}\) \(\log_{2}\frac{1}{4}\)

Show Answer

The answer is \(-2\)

Show Work

\(\,\,\,\,\,\log_{2}\frac{1}{4}=x\)

\(\,\,\,\,\,2^x=\frac{1}{4}\)

\(\,\,\,\,\,2^x=2^{-2}\)

\(\,\,\,\,\,x=-2\)

\(\textbf{18)}\) \(\log_{4}2\)

Show Answer

The answer is \(\frac{1}{2}\)

Show Work

\(\,\,\,\,\,\log_{4}2=x\)

\(\,\,\,\,\,4^x=2\)

\(\,\,\,\,\,\left(2^2\right)^x=2^1\)

\(\,\,\,\,\,2^{2x}=2^1\)

\(\,\,\,\,\,2x=1\)

\(\,\,\,\,\,x=\frac{1}{2}\)

Condensing Logarithms

Would you like to practice some?

\(\textbf{19)}\) Condense: \(\log_{5}(3) + \log_{5}(x)\)

Show Answer

The answer is \( \log_{5}(3x) \)

Show Work

\(\,\,\,\,\,\,\log_{b}(M) + \log_{b}(N) = \log_{b}(MN)\,\,\, \left(\text{Product Rule}\right)\)

\(\,\,\,\,\,\,\log_{5}(3) + \log_{5}(x) = \log_{5}(3x) \)

\(\textbf{20)}\) Condense: \(\ln(6) + \ln(y)\)

Show Answer

The answer is \( \ln(6y) \)

Show Work

\(\,\,\,\,\,\,\ln(M) + \ln(N) = \ln(MN)\,\,\, \left(\text{Product Rule}\right)\)

\(\,\,\,\,\,\,\ln(6) + \ln(y) = \ln(6y) \)

\(\textbf{21)}\) Condense: \(\log_{2}(x) – \log_{2}(4)\)

Show Answer

The answer is \( \log_{2}\left(\frac{x}{4}\right) \)

Show Work

\(\,\,\,\,\,\,\log_{b}(M) – \log_{b}(N) = \log_{b}\left(\frac{M}{N}\right)\,\,\, \left(\text{Quotient Rule}\right)\)

\(\,\,\,\,\,\,\log_{2}(x) – \log_{2}(4) = \log_{2}\left(\frac{x}{4}\right) \)

\(\textbf{22)}\) Condense: \(\ln(y) – \ln(10)\)

Show Answer

The answer is \( \ln\left(\frac{y}{10}\right) \)

Show Work

\(\,\,\,\,\,\,\ln(M) – \ln(N) = \ln\left(\frac{M}{N}\right)\,\,\, \left(\text{Quotient Rule}\right)\)

\(\,\,\,\,\,\,\ln(y) – \ln(10) = \ln\left(\frac{y}{10}\right) \)

\(\textbf{23)}\) Condense: \(4\log_{3}(x)\)

Show Answer

The answer is \( \log_{3}(x^4) \)

Show Work

\(\,\,\,\,\,\,p\log_{b}(M) = \log_{b}(M^p)\,\,\, \left(\text{Power Rule}\right)\)

\(\,\,\,\,\,\,4\log_{3}(x) = \log_{3}(x^4) \)

\(\textbf{24)}\) Condense: \(\frac{1}{3}\ln(y)\)

Show Answer

The answer is \( \ln(y^{\frac{1}{3}}) \)

Show Work

\(\,\,\,\,\,\,p\ln(M) = \ln(M^p)\,\,\, \left(\text{Power Rule}\right)\)

\(\,\,\,\,\,\,\frac{1}{3}\ln(y) = \ln(y^{\frac{1}{3}}) \)

\(\textbf{25)}\) Write as a single logarithmic expression.
\(2\log_{5}(2)+\frac{1}{2}\log_{5}(x+3)-\log_{5}(x) \)

Show Answer

The answer is \( \log_{5}\left(\frac{4\sqrt{x+3}}{x}\right) \)

Show Work

\(\,\,\,\,\,\,2\log_{5}(2)+\frac{1}{2}\log_{5}(x+3)-\log_{5}(x) \)

\(\,\,\,\,\,\,\log_{5}(2^2) + \log_{5}((x+3)^{\frac{1}{2}}) – \log_{5}(x) \)

\(\,\,\,\,\,\,\log_{5}(4) + \log_{5}\left((x+3)^{\frac{1}{2}}\right) – \log_{5}(x) \)

\(\,\,\,\,\,\,\log_{5}\left(\frac{4\sqrt{x+3}}{x}\right) \)

\(\textbf{26)}\) Write as a single logarithmic expression.
\(2\log_{b}(x)+\log_{b}(z)-5\log_{b}(y) \)

Show Answer

The answer is \( \displaystyle\log_{b}\left(\frac{x^2z}{y^5}\right) \)

Show Work

\(\,\,\,\,\,\,2\log_{b}(x)+\log_{b}(z)-5\log_{b}(y) \)

\(\,\,\,\,\,\,\log_{b}(x^2) + \log_{b}(z) – \log_{b}(y^5) \)

\(\,\,\,\,\,\,\log_{b}\left(x^2z\right) – \log_{b}(y^5) \)

\(\,\,\,\,\,\,\log_{b}\left(\frac{x^2z}{y^5}\right) \)

\(\textbf{27)}\) Write as a single logarithmic expression.
\(\frac{1}{3}\log_{5}(z)-5\log_{5}(y)-2 \)

Show Answer

The answer is \( \displaystyle\log_{5}\left(\frac{\sqrt[3]{z}}{25y^5}\right) \)

Show Work

\(\,\,\,\,\,\,\frac{1}{3}\log_{5}(z)-5\log_{5}(y)-2 \)

\(\,\,\,\,\,\,\log_{5}\left(z^{\frac{1}{3}}\right) – \log_{5}(y^5) – \log_{5}(25)\,\,\,\,\, \left(\text{note: } \log_{5}(25)=2\right) \)

\(\,\,\,\,\,\,\log_{5}\left(\frac{\sqrt[3]{z}}{25y^5}\right) \)

\(\textbf{28)}\) Write as a single logarithmic expression.
\(\log_{2}(b)+\frac{1}{2}\log_{2}(z)-5 \)

Show Answer

The answer is \( \log_{2}\left(\frac{b\sqrt{z}}{32}\right) \)

Show Work

\(\,\,\,\,\,\,\log_{2}(b)+\frac{1}{2}\log_{2}(z)-5 \)

\(\,\,\,\,\,\,\log_{2}(b) + \log_{2}(z^{\frac{1}{2}}) – \log_{2}(2^5) \)

\(\,\,\,\,\,\,\log_{2}(b) + \log_{2}(\sqrt{z}) – \log_{2}(2^5) \)

\(\,\,\,\,\,\,\log_{2}\left(b\sqrt{z}\right) – \log_{2}(32) \)

\(\,\,\,\,\,\,\log_{2}\left(\frac{b\sqrt{z}}{32}\right) \)

\(\textbf{29)}\) Write as a single logarithmic expression.
\(2\log_{5}(x)+5\log_{5}(2)-\frac{1}{2}\log_{5}(z) \)

Show Answer

The answer is \( \displaystyle\log_{5}\left(\frac{32x^2}{\sqrt{z}}\right) \)

Show Work

\(\,\,\,\,\,\,2\log_{5}(x)+5\log_{5}(2)-\frac{1}{2}\log_{5}(z) \)

\(\,\,\,\,\,\,\log_{5}(x^2) + \log_{5}(2^5) – \log_{5}(z^{\frac{1}{2}}) \)

\(\,\,\,\,\,\,\log_{5}(x^2) + \log_{5}(32) – \log_{5}(\sqrt{z}) \)

\(\,\,\,\,\,\,\log_{5}(32x^2) – \log_{5}(\sqrt{z}) \)

\(\,\,\,\,\,\,\log_{5}\left(\frac{32x^2}{\sqrt{z}}\right) \)

\(\textbf{30)}\) Write as a single logarithmic expression.
\(5\ln(x+2)-3\ln(y)-2\ln(z) \)

Show Answer

The answer is \( \displaystyle\ln\left(\frac{\left(x+2\right)^5}{y^3 z^2}\right) \)

Show Work

\(\,\,\,\,\,\,5\ln(x+2)-3\ln(y)-2\ln(z) \)

\(\,\,\,\,\,\,\ln((x+2)^5) – \ln(y^3) – \ln(z^2) \)

\(\,\,\,\,\,\,\ln\left(\frac{\left(x+2\right)^5}{y^3z^2}\right) \)

\(\textbf{31)}\) Write as a single logarithmic expression.
\(\frac{1}{4}\log(x)-8\log(z)+1 \)

Show Answer

The answer is \( \displaystyle\log\left(\frac{10\sqrt[4]{x}}{z^8}\right) \)

Show Work

\(\,\,\,\,\,\,\frac{1}{4}\log(x)-8\log(z)+1 \)

\(\,\,\,\,\,\,\log(x^{\frac{1}{4}}) – \log(z^8) + \log(10)\,\,\,\,\, \left(\text{note: } \log(10)=1\right)\)

\(\,\,\,\,\,\,\log(\sqrt[4]{x}) – \log(z^8) + \log(10) \)

\(\,\,\,\,\,\,\log\left(\frac{\sqrt[4]{x}}{z^8}\right) + \log(10) \)

\(\,\,\,\,\,\,\log\left(\frac{10\sqrt[4]{x}}{z^8}\right) \)

\(\textbf{32)}\) Simplify.
\(\log(8)+2\log(5)-\log(2) \)

Show Answer

The answer is \( 2 \)

Show Work

\(\,\,\,\,\,\,\log(8)+2\log(5)-\log(2) \)

\(\,\,\,\,\,\,\log(2^3) + \log(5^2) – \log(2) \)

\(\,\,\,\,\,\,3\log(2) + 2\log(5) – \log(2) \)

\(\,\,\,\,\,\,\log(2^{3-1}) + \log(25) \)

\(\,\,\,\,\,\,\log(4) + \log(25) \)

\(\,\,\,\,\,\,\log(4 \cdot 25) \)

\(\,\,\,\,\,\,\log(100) \)

\(\,\,\,\,\,\,2 \)

Expanding Logarithms

Would you like to practice some?

\(\textbf{33)}\) Expand: \(\log_{3}(2x)\)

Show Answer

The answer is \( \log_{3}(2) + \log_{3}(x) \)

Show Work

\(\,\,\,\,\,\,\log_{b}(MN) = \log_{b}(M) + \log_{b}(N)\,\,\, \left(\text{Product Rule}\right)\)

\(\,\,\,\,\,\,\log_{3}(2x) = \log_{3}(2) + \log_{3}(x) \)

\(\textbf{34)}\) Expand: \(\ln(7a)\)

Show Answer

The answer is \( \ln(7) + \ln(a) \)

Show Work

\(\,\,\,\,\,\,\ln(MN) = \ln(M) + \ln(N)\,\,\, \left(\text{Product Rule}\right)\)

\(\,\,\,\,\,\,\ln(7a) = \ln(7) + \ln(a) \)

\(\textbf{35)}\) Expand: \(\log_{2}\left(\frac{5}{x}\right)\)

Show Answer

The answer is \( \log_{2}(5) – \log_{2}(x) \)

Show Work

\(\,\,\,\,\,\,\log_{b}\left(\frac{M}{N}\right) = \log_{b}(M) – \log_{b}(N)\,\,\, \left(\text{Quotient Rule}\right)\)

\(\,\,\,\,\,\,\log_{2}\left(\frac{5}{x}\right) = \log_{2}(5) – \log_{2}(x) \)

\(\textbf{36)}\) Expand: \(\ln\left(\frac{y}{3}\right)\)

Show Answer

The answer is \( \ln(y) – \ln(3) \)

Show Work

\(\,\,\,\,\,\,\ln\left(\frac{M}{N}\right) = \ln(M) – \ln(N)\,\,\, \left(\text{Quotient Rule}\right)\)

\(\,\,\,\,\,\,\ln\left(\frac{y}{3}\right) = \ln(y) – \ln(3) \)

\(\textbf{37)}\) Expand: \(\log_{4}(x^2)\)

Show Answer

The answer is \( 2\log_{4}(x) \)

Show Work

\(\,\,\,\,\,\,\log_{b}(M^p) = p\log_{b}(M)\,\,\, \left(\text{Power Rule}\right)\)

\(\,\,\,\,\,\,\log_{4}(x^2) = 2\log_{4}(x) \)

\(\textbf{38)}\) Expand: \(\ln(y^3)\)

Show Answer

The answer is \( 3\ln(y) \)

Show Work

\(\,\,\,\,\,\,\ln(M^p) = p\ln(M)\,\,\, \left(\text{Power Rule}\right)\)

\(\,\,\,\,\,\,\ln(y^3) = 3\ln(y) \)

\(\textbf{39)}\) \( \displaystyle\log_{b}\left(\frac{x^2z}{y^5}\right) \)

Show Answer

The answer is \( 2\log_{b}(x)+\log_{b}(z)-5\log_{b}(y) \)

\(\textbf{40)}\) \( \displaystyle\log_{5}\left(\frac{\sqrt[3]{z}}{25y^5}\right) \)

Show Answer

The answer is \( \frac{1}{3}\log_{5}(z)-5\log_{5}(y)-2 \)

\(\textbf{41)}\) \( \displaystyle\log_{2}\left(\frac{b\sqrt{n}}{32}\right) \)

Show Answer

The answer is \( \log_{2}(b)+\frac{1}{2}\log_{2}(n)-5 \)

\(\textbf{42)}\) \( \log_{5}\left(\frac{4\sqrt{x+3}}{x}\right) \)

Show Answer

The answer is \( \displaystyle2\log_{5}(2)+\frac{1}{2}\log_{5}(x+3)-\log_{5}(x) \)

Show Work

\(\,\,\,\,\,\,\displaystyle\log_{5}\left(\frac{4\sqrt{x+3}}{x}\right) \)

\(\,\,\,\,\,\,\displaystyle\log_{5}\left(4\right) + \log_{5}\left(\sqrt{x+3}\right) – \log_{5}\left(x\right)\)

\(\,\,\,\,\,\,\displaystyle\log_{5}\left(2\right)^2 + \log_{5}(x+3)^{1/2} – \log_{5}\left(x\right)\)

\(\,\,\,\,\,\,2\log_{5}\left(2\right) + \frac{1}{2} \log_{5}(x+3) – \log_{5}\left(x\right)\)

Solving Logarithmic Equations

Lesson

Practice Problems & Videos

Solve for x.

\(\textbf{43)}\) \(\log_{3}x=2\)

Show Answer

\(x=9\)

Show Work

\(\,\,\,\,\,\,\log_{b}x=c \,\,\Rightarrow\,\, b^c=x\)

\(\,\,\,\,\,\,\log_{3}x=2 \,\,\Rightarrow \,\,3^2=x\)

\(\,\,\,\,\,\,x=9\)

\(\textbf{44)}\) \(\log_{2}(4x)=3\)

Show Answer

\(x=2\)

Show Work

\(\,\,\,\,\,\,\log_{b}x=c \,\,\Rightarrow\,\, b^c=x\)

\(\,\,\,\,\,\,\log_{2}(4x)=3 \,\,\Rightarrow \,\,2^3=4x\)

\(\,\,\,\,\,\,8=4x\)

\(\,\,\,\,\,\,2=x\)

\(\textbf{45)}\) \(\log_{4}(3x+1)=2\)

Show Answer

\(x=5\)

Show Work

\(\,\,\,\,\,\,\log_{b}x=c \,\,\Rightarrow\,\, b^c=x\)

\(\,\,\,\,\,\,\log_{4}(3x+1)=2 \,\,\Rightarrow \,\,4^2=3x+1\)

\(\,\,\,\,\,\,16=3x+1\)

\(\,\,\,\,\,\,15=3x\)

\(\,\,\,\,\,\,5=x\)

\(\textbf{46)}\) \(\log_{2}(5x)=\log_{2}(2x+12)\)

Show Answer

\(x=4\)

Show Work

\(\,\,\,\,\,\,\log_{2}(5x)=\log_{2}(2x+12)\)

\(\,\,\,\,\,\,5x=2x+12\)

\(\,\,\,\,\,\,3x=12\)

\(\,\,\,\,\,\,x=4\)

\(\textbf{47)}\) \(\log_{5}(x+1)+\log_{5}(4)=\log_{5}(24)\)

Show Answer

\(x=5\)

Show Work

\(\,\,\,\,\,\,\log_{5}(x+1)+\log_{5}(4)=\log_{5}(24)\)

\(\,\,\,\,\,\,\log_{5}(x+1)(4)=\log_{5}(24)\)

\(\,\,\,\,\,\,(x+1)(4)=(24)\)

\(\,\,\,\,\,\,4x+4=24\)

\(\,\,\,\,\,\,4x=20\)

\(\,\,\,\,\,\,x=5\)

\(\textbf{48)}\) \(\log_{6}(2x)+\log_{6}(x-1)=\log_{6}(10x)\)

Show Answer

\(x=6\)

Show Work

\(\,\,\,\,\,\,\log_{6}(2x)+\log_{6}(x-1)=\log_{6}(10x)\)

\(\,\,\,\,\,\,\log_{6}(2x)(x-1)=\log_{6}(10x)\)

\(\,\,\,\,\,\,(2x)(x-1)=(10x)\)

\(\,\,\,\,\,\,2x^2-2x=10x\)

\(\,\,\,\,\,\,2x^2-12x=0\)

\(\,\,\,\,\,\,x^2-6x=0\)

\(\,\,\,\,\,\,x(x-6)=0\)

\(\,\,\,\,\,\,x=0 \text{ or } x=6\)

\(\,\,\,\,\,\,x=0 \text{ is extraneous }\)

\(\,\,\,\,\,\,x=6\)

\(\textbf{49)}\) \(\log_{3}(4)-\log_{3}(x)=\log_{3}(2x-2)-\log_{3}(3x+4)\)

Show Answer

\(x=8\)

Show Work

\(\,\,\,\,\,\,\log_{3}(4)-\log_{3}(x)=\log_{3}(2x-2)-\log_{3}(3x+4)\)

\(\,\,\,\,\,\,\log_{3}\left(\frac{4}{x}\right)=\log_{3}\left(\frac{2x-2}{3x+4}\right)\)

\(\,\,\,\,\,\,\displaystyle\frac{4}{x}=\frac{2x-2}{3x+4}\)

\(\,\,\,\,\,\,(4)(3x+4)=(x)(2x-2)\)

\(\,\,\,\,\,\,12x+16=2x^2-2x\)

\(\,\,\,\,\,\,0=2x^2-14x-16\)

\(\,\,\,\,\,\,0=x^2-7x-8\)

\(\,\,\,\,\,\,0=(x-8)(x+1)\)

\(\,\,\,\,\,\,x=-1 \text{ or } x=8\)

\(\,\,\,\,\,\,x=-1 \text{ is extraneous}\)

\(\,\,\,\,\,\,x=8\)

\(\textbf{50)}\) \(\frac{1}{2}\log_{}(x^4)-\log_{}(2x-1)=\log_{}(x+2)-\log_{}(3)\)

Show Answer

\(x=1 \text{ or }x=2\)

Show Work

\(\,\,\,\,\,\,\frac{1}{2}\log_{}(x^4)-\log_{}(2x-1)=\log_{}(x+2)-\log_{}(3)\)

\(\,\,\,\,\,\,\log_{}\left(\sqrt{x^4}\right)-\log_{}(2x-1)=\log_{}(x+2)-\log_{}(3)\)

\(\,\,\,\,\,\,\log_{}\left(x^2\right)-\log_{}(2x-1)=\log_{}(x+2)-\log_{}(3)\)

\(\,\,\,\,\,\,\log_{}\left(\frac{x^2}{2x-1}\right)=\log_{}\left(\frac{x+2}{3}\right)\)

\(\,\,\,\,\,\,\displaystyle\frac{x^2}{2x-1}=\frac{x+2}{3}\)

\(\,\,\,\,\,\,3x^2=(x+2)(2x-1)\)

\(\,\,\,\,\,\,3x^2=2x^2+3x-2\)

\(\,\,\,\,\,\,x^2-3x+2=0\)

\(\,\,\,\,\,\,(x-1)(x-2)=0\)

\(\,\,\,\,\,\,x=1 \text{ or } x=2\)

\(\textbf{51)}\) \(\ln_{}(10x)=\ln_{}(4x+1)+\ln_{}(3-x)\)

Show Answer

\(x=1\)

Show Work

\(\,\,\,\,\,\ln_{}(10x)=\ln_{}(4x+1)+\ln_{}(3-x)\)

\(\,\,\,\,\,\ln_{}(10x)=\ln_{}(4x+1)(3-x)\)

\(\,\,\,\,\,10x=(4x+1)(3-x)\)

\(\,\,\,\,\,10x=-4x^2+11x+3\)

\(\,\,\,\,\,4x^2-x-3=0\)

\(\,\,\,\,\,(4x+3)(x-1)=0\)

\(\,\,\,\,\,x=-\frac{3}{4} \text{ or } x=1\)

\(\,\,\,\,\,x=-\frac{3}{4} \text{ is extraneous}\)

\(\,\,\,\,\,x=x=1\)

\(\textbf{52)}\) \(\log_{6}(8x-4)=2\)

Show Answer

\(x=5\)

Show Work

\(\,\,\,\,\,\,\log_{b}x=c \,\,\Rightarrow\,\, b^c=x\)

\(\,\,\,\,\,\,\log_{6}(8x-4)=2 \,\,\Rightarrow \,\,6^2=8x-4\)

\(\,\,\,\,\,\,36=8x-4\)

\(\,\,\,\,\,\,40=8x\)

\(\,\,\,\,\,\,5=x\)

\(\textbf{53)}\) \(\log_{7}(6x-5)=2\)

Show Answer

\(x=9\)

Show Work

\(\,\,\,\,\,\,\log_{b}x=c \,\,\Rightarrow\,\, b^c=x\)

\(\,\,\,\,\,\,\log_{7}(6x-5)=2 \,\,\Rightarrow \,\,7^2=6x-5\)

\(\,\,\,\,\,\,49=6x-5\)

\(\,\,\,\,\,\,54=6x\)

\(\,\,\,\,\,\,9=x\)

\(\textbf{54)}\) \(\log_{}(x-1)=\log_{}(5x)-1\)

Show Answer

\(x=2\)

Show Work

\(\,\,\,\,\,\,\log_{}(x-1)=\log_{}(5x)-1\)

\(\,\,\,\,\,\,\log_{}(x-1)=\log_{}(5x)-\log_{}(10)\)

\(\,\,\,\,\,\,\log_{}(x-1)=\log_{}\left(\frac{5x}{10}\right)\)

\(\,\,\,\,\,\,x-1=\displaystyle\frac{5x}{10}\)

\(\,\,\,\,\,\,x-1=\displaystyle\frac{x}{2}\)

\(\,\,\,\,\,\,2(x-1)=x\)

\(\,\,\,\,\,\,2x-2=x\)

\(\,\,\,\,\,\,x-2=0\)

\(\,\,\,\,\,\,x=2\)

\(\textbf{55)}\) \(\log_{4}(3x-10)=\log_{4}(8x)-2\)

Show Answer

\(x=4\)

Show Work

\(\,\,\,\,\,\,\log_{4}(3x-10)=\log_{4}(8x)-2\)

\(\,\,\,\,\,\,\log_{4}(3x-10)=\log_{4}(8x)-\log_{4}(16)\)

\(\,\,\,\,\,\,\log_{4}(3x-10)=\log_{4}\left(\frac{8x}{16}\right)\)

\(\,\,\,\,\,\,3x-10=\displaystyle\frac{8x}{16}\)

\(\,\,\,\,\,\,3x-10=\displaystyle\frac{x}{2}\)

\(\,\,\,\,\,\,2(3x-10)=x\)

\(\,\,\,\,\,\,6x-20=x\)

\(\,\,\,\,\,\,5x-20=0\)

\(\,\,\,\,\,\,5x=20\)

\(\,\,\,\,\,\,x=4\)

\(\textbf{56)}\) \(\log_{3}(x^2-2x)=\log_{3}(2-x)+2\)

Show Answer

\(x=-9\)

Show Work

\(\,\,\,\,\,\,\log_{3}(x^2-2x)=\log_{3}(2-x)+2\)

\(\,\,\,\,\,\,\log_{3}(x^2-2x)=\log_{3}(2-x)+\log_{3}(9)\)

\(\,\,\,\,\,\,\log_{3}(x^2-2x)=\log_{3}(2-x)(9)\)

\(\,\,\,\,\,\,x^2-2x=(2-x)(9)\)

\(\,\,\,\,\,\,x^2-2x=18-9x\)

\(\,\,\,\,\,\,x^2+7x-18=0\)

\(\,\,\,\,\,\,(x+9)(x-2)=0\)

\(\,\,\,\,\,\,x=-9 \text{ or } x=2\)

\(\,\,\,\,\,\,x=2 \text{ is extraneous }\)

\(\,\,\,\,\,\,x=-9\)

\(\textbf{57)}\) \(\log_{2}(x+1)+\log_{2}(x-1)=\log_{2}(2x+2)+1\)

Show Answer

\(\text{The answer is }x=5\)

Show Work

\(\,\,\,\,\,\,\log_{2}(x+1)+\log_{2}(x-1)=\log_{2}(2x+2)+1\)

\(\,\,\,\,\,\,\log_{2}(x+1)+\log_{2}(x-1)=\log_{2}(2x+2)+\log_{2}2\)

\(\,\,\,\,\,\,\log_{2}(x+1)(x-1)=\log_{2}(2x+2)(2)\)

\(\,\,\,\,\,\,(x+1)(x-1)=(2x+2)(2)\)

\(\,\,\,\,\,\,x^2-1=4x+4\)

\(\,\,\,\,\,\,x^2-4x-5=0\)

\(\,\,\,\,\,\,(x-5)(x+1)=0\)

\(\,\,\,\,\,\,x=-1 \,\text{ or }\, x=5\)

\(\,\,\,\,\,\,x=-1 \text{ is extraneous}\)

\(\,\,\,\,\,\,\text{The answer is }x=5\)

Change of Base Formula

The change of base formula allows you to rewrite logarithms in terms of logarithms with different bases, often using base 10 (\(\log\)) or base \(e\) (\(\ln\)). It is given by:

\(\log_{b}x = \frac{\log{x}}{\log{b}} \,\, \text{or} \,\, \log_{b}x = \frac{\ln{x}}{\ln{b}}\)

This is particularly useful for evaluating logarithms on calculators that may not directly support arbitrary bases. For example:

\(\log_{3}10 = \frac{\ln{10}}{\ln{3}} \approx 2.096\)

Practice Problems

\(\textbf{58)}\) Simplify \(\log_{4}{18}\) using the change of base formula.

Show Answer

The answer is \(\frac{\ln{18}}{\ln{4}} \approx 2.085\)

\(\textbf{59)}\) Simplify \(\log_{7}{49}\) using the change of base formula.

Show Answer

The answer is \(\frac{\ln{49}}{\ln{7}} = 2\)

\(\textbf{60)}\) Simplify \(\log_{5}{125}\) using the change of base formula.

Show Answer

The answer is \(\frac{\ln{125}}{\ln{5}} = 3\)

\(\textbf{61)}\) Simplify \(\log_{8}{32}\) using the change of base formula.

Show Answer

The answer is \(\frac{\ln{32}}{\ln{8}} \approx 1.667\)

\(\textbf{62)}\) Simplify \(\log_{2}{50}\) using the change of base formula.

Show Answer

The answer is \(\frac{\ln{50}}{\ln{2}} \approx 5.644\)

Natural Logarithms

Natural logarithms use the base \(e\), where \(e \approx 2.71828\). They are denoted as \(\ln\). For example:

\(\ln{x} \,\, \text{is equivalent to} \,\, \log_{e}x.\)

Natural logs are widely used in mathematics, they have applications in exponential growth and decay models.

Practice Problems

\(\textbf{63)}\) Solve \(\ln{(x+2)} = 3\).

Show Answer

The answer is \(x = e^3 – 2 \approx 18.085\)

Show Work

\(\,\,\,\,\,\,\ln{(x+2)} = 3\)

\(\,\,\,\,\,\,\text{Rewrite } \ln{(x+2)} \text{ as } \log_{e}{(x+2)}:\)

\(\,\,\,\,\,\,\log_{e}{(x+2)} = 3\)

\(\,\,\,\,\,\,\text{Rewrite using the definition of logarithms: } e^3 = x+2\)

\(\,\,\,\,\,\,x+2 = e^3\)

\(\,\,\,\,\,\,x = e^3 – 2\)

\(\,\,\,\,\,\,x \approx 18.085\)

\(\textbf{64)}\) Solve \(\ln{(3x)} = 5\).

Show Answer

The answer is \(x = \frac{e^5}{3} \approx 49.471\)

Show Work

\(\,\,\,\,\,\,\ln{(3x)} = 5\)

\(\,\,\,\,\,\,\text{Rewrite } \ln{(3x)} \text{ as } \log_{e}{(3x)}:\)

\(\,\,\,\,\,\,\log_{e}{(3x)} = 5\)

\(\,\,\,\,\,\,\text{Rewrite using the definition of logarithms: } e^5 = 3x\)

\(\,\,\,\,\,\,3x = e^5\)

\(\,\,\,\,\,\,x = \frac{e^5}{3}\)

\(\,\,\,\,\,\,x \approx 49.471\)

\(\textbf{65)}\) Solve \(\ln{(x-4)} = 2\).

Show Answer

The answer is \(x = e^2 + 4 \approx 11.389\)

Show Work

\(\,\,\,\,\,\,\ln{(x-4)} = 2\)

\(\,\,\,\,\,\,\text{Rewrite } \ln{(x-4)} \text{ as } \log_{e}{(x-4)}:\)

\(\,\,\,\,\,\,\log_{e}{(x-4)} = 2\)

\(\,\,\,\,\,\,\text{Rewrite using the definition of logarithms: } e^2 = x-4\)

\(\,\,\,\,\,\,x-4 = e^2\)

\(\,\,\,\,\,\,x = e^2 + 4\)

\(\,\,\,\,\,\,x \approx 11.389\)

\(\textbf{66)}\) Solve \(\ln{(5x-1)} = 4\).

Show Answer

The answer is \(x = \frac{e^4 + 1}{5} \approx 11.120\)

Show Work

\(\,\,\,\,\,\,\ln{(5x-1)} = 4\)

\(\,\,\,\,\,\,\text{Rewrite } \ln{(5x-1)} \text{ as } \log_{e}{(5x-1)}:\)

\(\,\,\,\,\,\,\log_{e}{(5x-1)} = 4\)

\(\,\,\,\,\,\,\text{Rewrite using the definition of logarithms: } e^4 = 5x-1\)

\(\,\,\,\,\,\,5x-1 = e^4\)

\(\,\,\,\,\,\,5x = e^4 + 1\)

\(\,\,\,\,\,\,x = \frac{e^4 + 1}{5}\)

\(\,\,\,\,\,\,x \approx 11.120\)

\(\textbf{67)}\) Solve \(\ln{(2x+3)} = 6\).

Show Answer

The answer is \(x = \frac{e^6 – 3}{2} \approx 200.214\)

Show Work

\(\,\,\,\,\,\,\ln{(2x+3)} = 6\)

\(\,\,\,\,\,\,\text{Rewrite } \ln{(2x+3)} \text{ as } \log_{e}{(2x+3)}:\)

\(\,\,\,\,\,\,\log_{e}{(2x+3)} = 6\)

\(\,\,\,\,\,\,\text{Rewrite using the definition of logarithms: } e^6 = 2x+3\)

\(\,\,\,\,\,\,2x+3 = e^6\)

\(\,\,\,\,\,\,2x = e^6 – 3\)

\(\,\,\,\,\,\,x = \frac{e^6 – 3}{2}\)

\(\,\,\,\,\,\,x \approx 200.214\)

Extraneous Solutions and Domain Restrictions

When solving logarithmic equations, extraneous solutions may arise. These are solutions that do not satisfy the domain of the original logarithmic expression. Remember:

The domain of a logarithmic function \(\log_{b}{x}\) is \(x > 0\).

Check all solutions to ensure they are within the domain.

See Related Pages\(\)

\(\bullet\text{ Evaluating Logarithms}\)
\(\,\,\,\,\,\,\,\,\log_{2}(8)…\)

\(\bullet\text{ Decibel Problems}\)
\(\,\,\,\,\,\,\,\,N_{dB}=10\log \left(\frac{P}{10^{-12}}\right)…\)

\(\bullet\text{ Earthquake Problems}\)
\(\,\,\,\,\,\,\,\,M=\log\frac{I}{10^{-4}}…\)

\(\bullet\text{ Domain and Range Logarithmic Functions}\)
\(\,\,\,\,\,\,\,\,f(x)=log(x) \rightarrow \text{Domain:} x\gt0… \)

\(\bullet\text{ Graphing Logarithmic Functions}\)
\(\,\,\,\,\,\,\,\,f(x)=log_{2}(x)\)

\(\bullet\text{ Solving Logarithmic Equations}\)
\(\,\,\,\,\,\,\,\,\log_{2}(5x)=\log_{2}(2x+12)…\)

\(\bullet\text{ Inverse of Logarithmic Functions}\)
\(\,\,\,\,\,\,\,\,f(x)=log_{2}(x) \rightarrow f^{-1}(x)=2^x\)

\(\bullet\text{ Half Life Questions}\)
\(\,\,\,\,\,\,\,\,A_t=A_0e^{kt}\)

\(\bullet\text{ Compound Interest}\)
\(\,\,\,\,\,\,\,\,A=P\left(1+\frac{r}{n} \right)^{nt}\,\,\,\,\,\,\,\,A=P e^{rt}\)

About Andymath.com

Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.

Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.

Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!

Thank you for visiting. How exciting!