Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?

Notes

Problems & Solutions

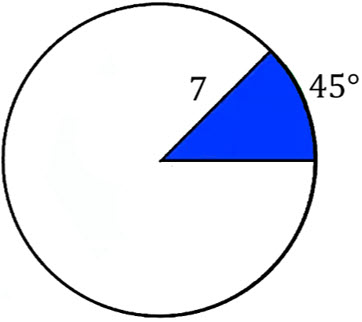
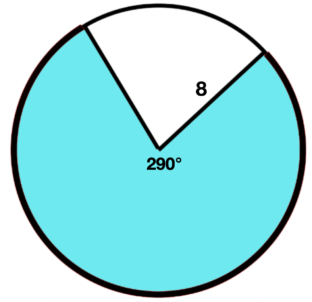
\(\textbf{1)}\) Find the area of the shaded sector.

Show Area of Sector

The area is \(\frac{49}{8} \pi \approx19.24\)

Show Work

\(\,\,\,\text{Area}=\displaystyle\frac{n^{\circ}}{360^{\circ}}\cdot \pi r^2\)

\(\,\,\,\displaystyle\frac{45^{\circ}}{360^{\circ}}\cdot \pi 7^2\)

\(\,\,\,\displaystyle\frac{1}{8}\cdot \pi 7^2\)

\(\,\,\,\displaystyle\frac{1}{8}\cdot \pi 49\)

\(\,\,\,\)The area is \(\frac{49}{8} \pi \approx19.24\)

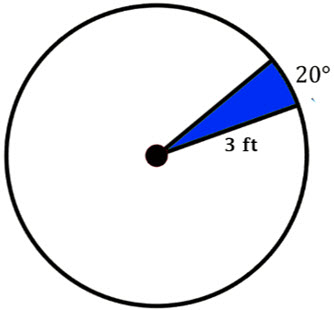
\(\textbf{2)}\) Find the area of the shaded sector.

Show Area of Sector

The area is \(\frac{1}{2} \pi\) ft\(^2\approx1.57\) ft\(^2\)

Show Work

\(\,\,\,\text{Area}=\displaystyle\frac{n^{\circ}}{360^{\circ}}\cdot \pi r^2\)

\(\,\,\,\,\,\,\,\,\,\displaystyle\frac{20^{\circ}}{360^{\circ}}\cdot \pi (3)^2\)

\(\,\,\,\,\,\,\,\,\,\displaystyle\frac{1}{18}\cdot \pi \cdot 9\)

\(\,\,\,\,\,\,\,\,\,\displaystyle\frac{9}{18}\cdot \pi\)

\(\,\,\,\,\,\,\,\,\,\displaystyle\frac{1}{2}\cdot \pi\)

\(\)The area is \(\frac{1}{2} \pi\) ft\(^2\approx1.57\) ft\(^2\)

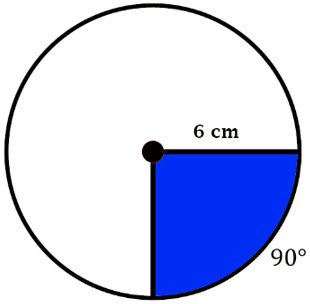
\(\textbf{3)}\) Find the area of the shaded sector.

Show Area of Sector

The area is \(9\pi\) cm\(^2\approx 28.27\) cm\(^2\)

Show Work

\(\,\,\,\text{Area}=\displaystyle\frac{n^{\circ}}{360^{\circ}}\cdot \pi r^2\)

\(\,\,\,\text{Area}=\displaystyle\frac{(90)^{\circ}}{360^{\circ}}\cdot \pi (6)^2\)

\(\,\,\,\text{Area}=\displaystyle\frac{1}{4}\cdot 36 \pi\)

\(\,\,\,\text{Area}=\displaystyle 9 \pi\)

\(\,\,\,\text{Area}=\displaystyle 9 \pi\)

\(\,\,\,\text{The area is } 9\pi\) cm\(^2\approx 28.27\) cm\(^2\)

\(\textbf{4)}\) Find the area of the shaded sector.

Show Area of Sector

The area is \(\displaystyle\frac{430 \pi}{9}\) units\(^2 \approx 150.098\) units\(^2\)

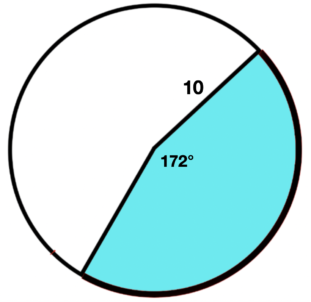
\(\textbf{5)}\) Find the area of the shaded sector.

Show Area of Sector

The area is \(\displaystyle\frac{392\pi}{9}\) units\(^2\approx 136.834\) units\(^2\)

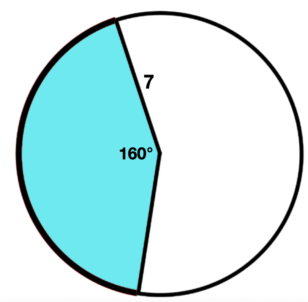
\(\textbf{6)}\) Find the area of the shaded sector.

Show Area of Sector

The area is \(\displaystyle\frac{275\pi}{36}\) units\(^2\approx 23.998\) units\(^2\)

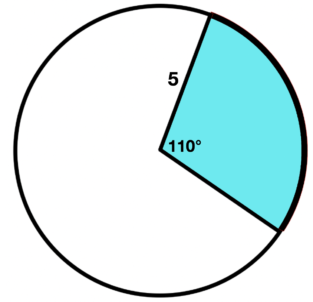
\(\textbf{7)}\) Find the area of the shaded sector.

Show Area of Sector

The area is \(\displaystyle\frac{121\pi}{2}\) units\(^2\approx 190.066\) units\(^2\)

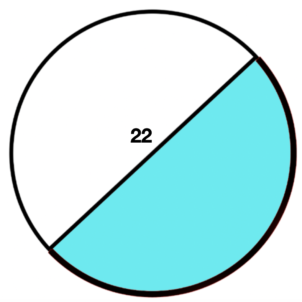
\(\textbf{8)}\) Find the area of the shaded sector.

Show Area of Sector

The area is \(\displaystyle\frac{464\pi}{9}\) units\(^2\approx 161.967\) units\(^2\)

See Related Pages\(\)

\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)

\(\bullet\text{ Notes- Segments and Angles in Circles}\)
\(\,\,\,\,\,\,\,\,\)

\(\bullet\text{ Area and Circumference of a Circle}\)
\(\,\,\,\,\,\,\,\,A=\pi r^2, \,\,\, C=2 \pi r\)

\(\bullet\text{ Equation of a Circle}\)
\(\,\,\,\,\,\,\,\,(x-h)^2+(y-k)^2=r^2\)

In Summary

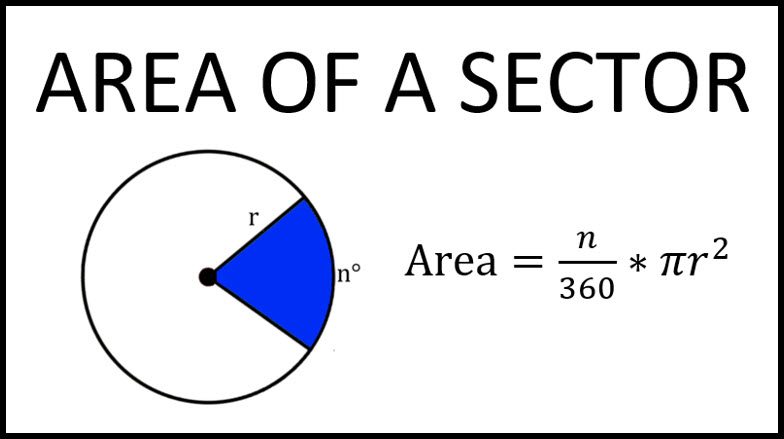
An area of a sector is a portion of the area of a circle that is bounded by two radii and an arc. A slice of pizza is a real world example of a sector. It is used to find the size of a region within a circle when given certain information such as the radius and the measure of the central angle of the sector. Area of a sector is typically taught in geometry classes, specifically in the study of circles.

Math topics related to the Area of a Sector

Radius and diameter of a circle: The radius of a circle is the distance from the center of the circle to any point on the circumference, while the diameter is the distance across the circle passing through the center. Both the radius and diameter are important when calculating the area of a sector.

Area of a circle: The area of a circle is the space contained within the circumference of the circle. It is calculated by multiplying the radius of the circle by itself and then by the value of π. The area of a circle is an important concept in geometry and is used in many real-world applications

Circumference of a circle: The circumference of a circle is the distance around the circle and is calculated using the formula C = 2πr, where r is the radius of the circle. The circumference can be found using the area of a sector if the radius and measure of the central angle of the sector are known.

Arc length: The arc length of a sector is the distance along the curved line formed by the sector. It can be calculated using the formula L = (θ/360) * C, where θ is the measure of the central angle of the sector in degrees and C is the circumference of the circle.

Central angle of a circle: The central angle of a circle is the angle formed by two radii of the circle. The measure of the central angle is an important factor in calculating the area of a sector.

About Andymath.com

Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.

Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.

Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!

Thank you for visiting. How exciting!