Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Practice Problems
For each rational function, identify the vertical asymptotes.
\(\textbf{1)}\) \(f(x)= \displaystyle\frac{4x+5}{x+1}\)
\(\textbf{2)}\) \(f(x)= \displaystyle\frac{5}{x^2-4}\)![Link to Youtube Video Solving Question Number 2](https://andymath.com/wp-content/uploads/2020/08/play-video.jpg")
\(\textbf{3)}\) \(f(x)= \displaystyle\frac{x^2-9}{x^2-3x}\)
\(\textbf{4)}\) \(f(x)= \displaystyle\frac{2x+5}{4x-3}\)
\(\textbf{5)}\) \(f(x)= \displaystyle\frac{4x}{x^2+4x+4}\)
\(\textbf{6)}\) \(f(x)= \displaystyle\frac{x^2+6x+9}{x^2-9}\)
\(\textbf{7)}\) \(f(x)= \displaystyle\frac{x^2+3x+2}{5x+5}\)
\(\textbf{8)}\) \(f(x)= \displaystyle\frac{x^3-1}{x^2-1}\)
Challenge Problems
\(\textbf{9)}\) \(f(x)= \displaystyle\frac{x^2-1}{x^4-1}\)
\(\textbf{10)}\) \(f(x)= \displaystyle\frac{x^3-8}{x^2+2x+4}\)
See Related Pages\(\)
\(\bullet\text{ Asymptotes Calculator (Mathway.com) }\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Horizontal Asymptotes}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Slant Asymptotes}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Graphing Rational Functions}\)
\(\,\,\,\,\,\,\,\,f(x)= \displaystyle\frac{4x+5}{x+1}\)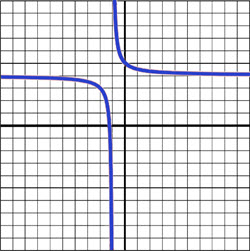
In Summary
Vertical asymptotes are vertical lines on a graph that a function arbitrarily close to, but never intersects, the function becomes infinitely large (or small) as it approaches the asymptote, but never actually reaches it. They are represented by a dashed line on a graph.
Vertical asymptotes are typically learned in algebra 2 or precalculus when studying the graphs of rational expressions.
One common mistake when working with vertical asymptotes is confusing them with removable discontinuities (or holes). While both signify discontinuity in the graph, they are very different things and have different effects on the shape of the graph.
Real world examples of Vertical Asymptotes
The speed of sound in air as the temperature approaches absolute zero. As the temperature gets colder and colder, the speed of sound approaches the asymptote of zero, but never actually reaches it.
The rate of decay of radioactive substances. As the amount of a radioactive substance decreases over time, the rate of decay approaches zero, but never actually reaches it.
The rate of economic growth as the population approaches the carrying capacity of the environment. As the population approaches the maximum number of individuals that can be supported by the available resources, the rate of economic growth approaches zero, but never actually reaches it.
The rate of change in the concentration of a chemical in a solution as it approaches equilibrium. As the concentration of the chemical approaches the equilibrium concentration, the rate of change approaches zero, but never actually reaches it.
The resistance of a conductor as the temperature approaches absolute zero. As the temperature gets colder and colder, the resistance of the conductor approaches the asymptote of zero, but never actually reaches it.
Math topics that use Vertical Asymptotes
Limits: Vertical asymptotes show up in infinite limits. For example, if a function has a vertical asymptote at x = 3, the limit of the function as x approaches 3 needs to be analyzed from both sides to see if the limit exists.
Slope fields: Vertical asymptotes can show up in slope fields, which are graphical representations of differential equations. Slope fields can be used to understand the behavior of a function and predict its future behavior.
Rational functions: Vertical asymptotes are often found in rational functions, which are functions that can be expressed as the ratio of two polynomials. The asymptotes of a rational function can be found by (after removing any holes) setting the denominator of the function equal to zero and solving for the x-values.
Graph sketching: Vertical asymptotes can be used to sketch the graph of a function. By identifying the asymptotes of a function, you can get a sense of its overall shape and behavior.
Continuity and discontinuity: Vertical asymptotes can be used to determine whether a function is continuous or discontinuous. If a function has a vertical asymptote, it is discontinuous at that point.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!