Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Notes
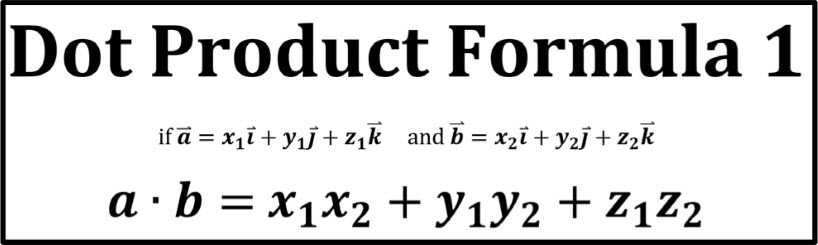
Questions & Answers
\(\textbf{1)}\) Let \(\vec{u}=2\vec{i}-3\vec{j}\) and \(\vec{v}=4\vec{i} +2\vec{j}\).
Find the dot product \( \vec{u} \cdot \vec{v} \)
\(\textbf{2)}\) Let \(\vec{u}=2\vec{i}-3\vec{j}\) and \(\vec{v}=4\vec{i} +2\vec{j}\).
Find the angle between \( \vec{u} \) and \( \vec{v} \)
\(\textbf{3)}\) Let \(\vec{r}=2\vec{i}+5\vec{j}-1\vec{k}\) and \(\vec{s}=3\vec{i}-4\vec{j}+6\vec{k}\).
Find the dot product \( \vec{r} \cdot \vec{s} \)
\(\textbf{4)}\) Let \(\vec{r}=2\vec{i}+5\vec{j}-1\vec{k}\) and \(\vec{s}=3\vec{i}-4\vec{j}+6\vec{k}\).
Find the angle between \( \vec{r} \) and \( \vec{s} \)
\(\textbf{5)}\) \( |\vec{n}|=4, |\vec{c}|=8, \) and the angle between the two vectors when placed tail to tail is \( 52^{\circ}. \) Find the Dot Product \( \vec{n} \cdot \vec{c} \)
\(\textbf{6)}\) Find the dot product of the two vectors in the picture below.

\(\textbf{7)}\) Find k so that \( \vec{u}=(2,3,4) \) and \( \vec{v}=(-5,k,1) \) are orthogonal.
See Related Pages\(\)
\(\bullet\text{ Displacement Vectors}\)
\(\,\,\,\,\,\,\,\,(x_2-x_1)\vec{i}+(y_2-y_1)\vec{j}…\)
\(\bullet\text{ Magnitude, Direction, and Unit Vectors}\)
\(\,\,\,\,\,\,\,\,|\vec{u}|=\sqrt{a^2+b^2}…\)
\(\bullet\text{ Dot Product}\)
\(\,\,\,\,\,\,\,\,a \cdot b=x_1 x_2+ y_1 y_2…\)
\(\bullet\text{ Parallel and Perpendicular Vectors}\)
\(\,\,\,\,\,\,\,\,⟨8,2⟩ \text{ and } ⟨−4,−1⟩…\)
\(\bullet\text{ Scalar and Vector Projections}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{a \cdot b}{|b|^2} \, \vec{b}…\)
\(\bullet\text{ Cross Product}\)
\(\,\,\,\,\,\,\,\,\)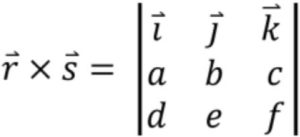 \(…\)
\(…\)
\(\bullet\text{ Equation of a Plane}\)
\(\,\,\,\,\,\,\,\,Ax+By+Cz=D…\)
\(\bullet\text{ Andymath Homepage}\)
In Summary
The dot product, aka the scalar product, aka the inner product, is a mathematical operation that takes two vectors and returns a scalar value. It is a fundamental concept in linear algebra and is often used in physics and engineering to calculate the projection of one vector onto another. The dot product can be calculated two different ways.
Algebraic Formula:
If we have two vectors in three-dimensional space: \(A = (a_1, a_2, a_3) and B = (b_1, b_2, b_3)\). The dot product of A and B is calculated using the following algebraic formula:
\(A \cdot B = (a_1)(b_1) + (a_2)(b_2) + (a_3)(b_3)\)
Geometric Formula:
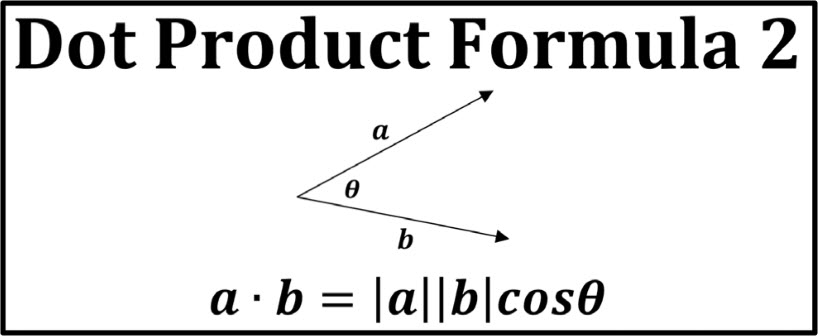
Another way to calculate the dot product is based on the magnitudes of the vectors and the angle \(\theta\) between them. If \(|A|\) represents the magnitude (length) of vector \(A\), and \(|B|\) represents the magnitude of vector \(B\), and \(\theta\) is the angle between the two vectors, then the dot product can be calculated using the following formula:
\(A \cdot B = |A| |B| \cos(\theta)\)
Both formulas yield the same result for the dot product of two vectors. Depending on the context and available information, you can choose the most suitable formula for your calculations. Or use both equations to find a missing piece of information in one of the formulas.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!