The eccentricity of a conic section is a measure of how much the shape deviates from a circle.

If two conic sections have the same eccentricity, then they are similar.

Notes

\(\text{Eccentricity}=\displaystyle\frac{\text{Distance from Center to Focus (c)}}{\text{Distance from Center to Vertex (a)}}\)

\({\text{Conic Sections & Eccentricity}}\)
\(\underline{\text{Conic Section}}\)	\(\underline{\text{Eccentricity (e)}}\)
\(\text{Circle}\)	\(e=0\)
\(\text{Ellipse}\)	\(0 \lt e \lt 1\)
\(\text{Parabola}\)	\(e=1\)
\(\text{Hyperbola}\)	\(e \gt 1\)

\({\text{Ellipses}}\)
\(\text{Equation}\)	\(\displaystyle\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\) \(a\gt b\)	\(\displaystyle\frac{(x-h)^2}{b^2}+\frac{(y-k)^2}{a^2}=1\) \(a\gt b\)
\(\text{Shape}\)
\(\text{Foci}\)	\((h \pm c,k)\)	\((h ,k \pm c)\)
\(\text{Vertices}\)	\((h \pm a,k)\)	\((h ,k \pm a)\)
\(\text{Center}\)	\((h,k)\)
\(\text{Focal Length Equation}\)	\(a^2-b^2=c^2\)
\(\text{Length of Major Axis}\)	\(2a\)
\(\text{Length of Minor Axis}\)	\(2b\)
\(\text{Eccentricity}\)	\(\displaystyle\frac{c}{a}\)

Practice Problems

\(\textbf{1)}\) Find the eccentricity of the following circle.
\(\displaystyle(x-4)^2+y^2=16\)

Show Eccentricity

The eccentricity is \( e=0 \)

Show Work

All Circles have eccentricity \( e=0 \)

\(\textbf{2)}\) Find the eccentricity of the following ellipse.
\(\displaystyle\frac{x^2}{16}+\displaystyle\frac{y^2}{25}=1\)

Show Eccentricity

\(\,\,\,\)The eccentricity is \( e=\displaystyle\frac{3}{5} \)

Show Work

\(\,\,\,\text{For ellipses, } a^2-b^2=c^2\)

\(\,\,\, 25-16=c^2\)

\(\,\,\, 9=c^2\)

\(\,\,\, c=3\)

\(\,\,\, e=\displaystyle \frac{c}{a}\)

\(\,\,\, e=\displaystyle \frac{3}{5}\)

\(\textbf{3)}\) Find the eccentricity of the following parabola.
\(\displaystyle y= 4(x+2)^2+3\)

Show Eccentricity

The eccentricity is \( e=1 \)

Show Work

All Parabolas have eccentricity \( e=1 \)

\(\textbf{4)}\) Find the eccentricity of the following hyperbola.
\(\displaystyle\frac{x^2}{144}-\displaystyle\frac{y^2}{25}=1\)

Show Eccentricity

\(\,\,\,\)The eccentricity is \( e=\displaystyle\frac{13}{12} \)

Show Work

\(\,\,\,\text{For hyperbolas, } a^2+b^2=c^2\)

\(\,\,\, 144+25=c^2\)

\(\,\,\, 169=c^2\)

\(\,\,\, c=13\)

\(\,\,\, e=\displaystyle \frac{c}{a}\)

\(\,\,\, e=\displaystyle \frac{13}{12}\)

Challenge Problem

\(\textbf{5)}\) Find the equation of the ellipse with vertices at (-10, 0) and (10, 0) with an eccentricity of \(\frac{3}{5}\).

Show Equation

\(\,\,\,\)The equation is \(\displaystyle\frac{x^2}{100}+\frac{y^2}{64}=1 \)

Show Work

\(\,\,\,\left(\text{Center is Midpoint of Vertices}\right)\,\,\, \displaystyle\left(\frac{-10+10}{2},\frac{0-0}{2}\right)=\left(0,0\right)\)

\(\,\,\,\left(a= \text{Distance from Center to a Vertex}\right)\,\,\, a=10\)

\(\,\,\,\left(\text{Eccentricity Formula}\right)\,\,\, \displaystyle e=\frac{c}{a}\)

\(\,\,\,\left(\text{Fill in } e \text{ and } a\right),\,\,\, \displaystyle \frac{3}{5}=\frac{c}{10}\)

\(\,\,\,\left(\text{Cross Multiply}\right)\,\,\, \displaystyle 30=5c\)

\(\,\,\, c=6\)

\(\,\,\,\left(\text{For ellipses}\right)\,\,\, a^2-b^2=c^2\)

\(\,\,\, 100-b^2=36\)

\(\,\,\, b^2=64\)

\(\,\,\, b=8\)

\(\,\,\,\left(\text{Equation Horizontal Ellipses}\right)\,\,\, \displaystyle\frac{\left(x-h\right)^2}{a^2}+\frac{\left(y-k\right)^2}{b^2}=1\)

\(\,\,\,\left(\text{Fill in what we know.}\right)\,\,\, \displaystyle\frac{(x-0)^2}{100}+\frac{(y-0)^2}{64}=1\)

\(\,\,\,\left(\text{Clean it up}\right) \displaystyle\frac{x^2}{100}+\frac{y^2}{64}=1\)

See Related Pages\(\)

\(\bullet\text{ All Conic Section Notes}\)
\(\,\,\,\,\,\,\,\,\)

\(\bullet\text{ Equation of a Circle}\)
\(\,\,\,\,\,\,\,\,(x-h)^2+(y-k)^2=r^2…\)

\(\bullet\text{ Parabolas}\)
\(\,\,\,\,\,\,\,\,y=a(x-h)^2+k…\)

\(\bullet\text{ Axis of Symmetry}\)
\(\,\,\,\,\,\,\,\,x=-\frac{b}{2a}…\)

\(\bullet\text{ Ellipses}\)
\(\,\,\,\,\,\,\,\,\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1…\)

\(\bullet\text{ Area of Ellipses}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\pi a b…\)

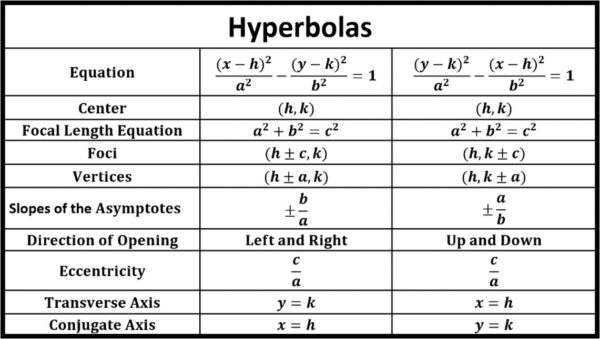
\(\bullet\text{ Hyperbolas}\)
\(\,\,\,\,\,\,\,\,\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1…\)

\(\bullet\text{ Conic Sections- Completing the Square}\)
\(\,\,\,\,\,\,\,\,x^2+8x+y^2−6y=11 \Rightarrow (x+4)^2+(y−3)^2=36…\)

\(\bullet\text{ Conic Sections- Parametric Equations}\)
\(\,\,\,\,\,\,\,\,x=h+r \cos{t}\)
\(\,\,\,\,\,\,\,\,y=k+r \sin{t}…\)

\(\bullet\text{ Degenerate Conics}\)
\(\,\,\,\,\,\,\,\,x^2−y^2=0…\)

\(\bullet\text{ Andymath Homepage}\)

About Andymath.com

Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.

Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.

Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!

Thank you for visiting. How exciting!