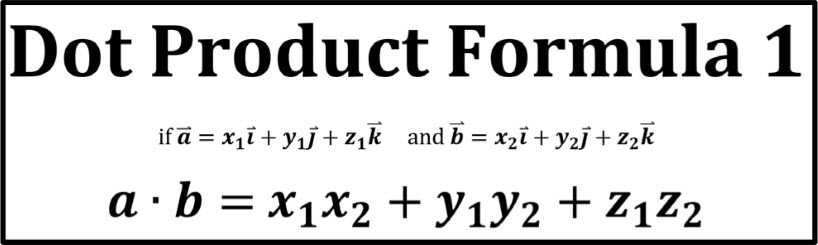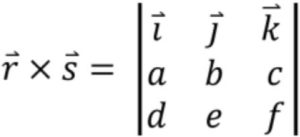Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Notes
Orthogonal Vectors
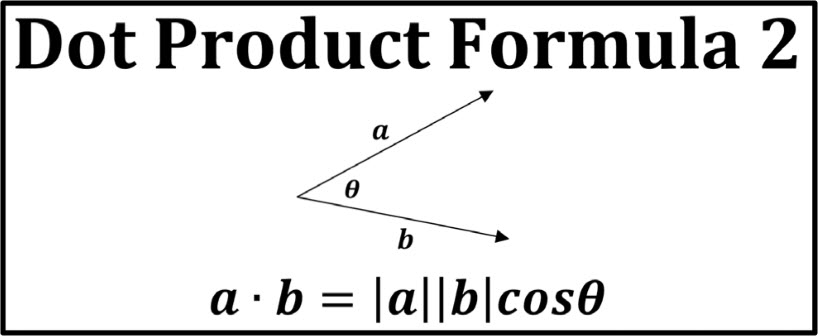
Dot Product \(\vec{u} \cdot \vec{v}=0\)
Practice Problems
\(\textbf{1)}\) Are \( \vec{u}=(1,2,3) \) and \( \vec{v}=(8,-4,0) \) orthogonal?
\(\textbf{2)}\) Are \( \vec{u}=(1,5,8) \) and \( \vec{v}=(3,-5,1) \) orthogonal?
\(\textbf{3)}\) Are \( \vec{u}=-5,-4,10) \) and \( \vec{v}=4,5,4) \) orthogonal?
\(\textbf{4)}\) Are \( \vec{u}=(-2,3,5) \) and \( \vec{v}=(5,4,2) \) orthogonal?
Challenge Problem
\(\textbf{5)}\) Find k so that \( \vec{u}=(2,3,4) \) and \( \vec{v}=(-5,k,1) \) are orthogonal.
See Related Pages\(\)
\(\bullet\text{ Displacement Vectors}\)
\(\,\,\,\,\,\,\,\,(x_2-x_1)\vec{i}+(y_2-y_1)\vec{j}…\)
\(\bullet\text{ Magnitude, Direction, and Unit Vectors}\)
\(\,\,\,\,\,\,\,\,|\vec{u}|=\sqrt{a^2+b^2}…\)
\(\bullet\text{ Dot Product}\)
\(\,\,\,\,\,\,\,\,a \cdot b=x_1 x_2+ y_1 y_2…\)
\(\bullet\text{ Parallel and Perpendicular Vectors}\)
\(\,\,\,\,\,\,\,\,⟨8,2⟩ \text{ and } ⟨−4,−1⟩…\)
\(\bullet\text{ Scalar and Vector Projections}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{a \cdot b}{|b|^2} \, \vec{b}…\)
\(\bullet\text{ Cross Product}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
\(\bullet\text{ Equation of a Plane}\)
\(\,\,\,\,\,\,\,\,Ax+By+Cz=D…\)
In Summary
Orthogonal vectors are two or more vectors that are perpendicular to each other. In mathematical terms, orthogonal vectors are defined as vectors that have a dot product of zero. This means that if you multiply the components of the two vectors together and add them up, the result is zero.
Orthogonal vectors are typically studied in linear algebra classes, and are very important in math, engineering and physics.
A fun fact about orthogonal vectors is that they are often used to describe the orientation of planes in three-dimensional space. For example, the three axes of a coordinate system (x, y, and z) are all orthogonal to each other.
Some related topics to orthogonal vectors include linear independence, basis vectors, and projection.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!