Practice Problems

\(\textbf{1)}\) The length of a rectangle is 3 times its width. The area of the rectangle is 48 square yards. Find the dimensions of the rectangle.

Show Answer

\( \text{Width} = 4 \text{ yards}, \text{Length} = 12 \text{ yards} \)

Show Work

\(\,\,\,\,\, \text{Length } (l) \, \times \, \text{Width } (w) = \text{Area } (A)\)

\(\,\,\,\,\, l=3w, \, A=48\)

\(\,\,\,\,\, \left(3w\right)\left(w\right)=48\)

\(\,\,\,\,\, 3w^2=48\)

\(\,\,\,\,\, w^2=16\)

\(\,\,\,\,\, w=\pm4\)

\(\,\,\,\,\, w=4\)

\(\,\,\,\,\, l=3(4)=12\)

\(\,\,\,\,\, \text{Width} = 4 \text{ yards}, \text{Length} = 12 \text{ yards} \)

\(\textbf{2)}\) The length of a rectangle is 4 times its width. The area of the rectangle is 100 square feet. Find the dimensions of the rectangle.

Show Answer

\( \text{Width} = 5 \text{ ft}, \text{Length} = 20 \text{ ft} \)

Show Work

\(\,\,\,\,\, \text{Length } (l) \, \times \, \text{Width } (w) = \text{Area } (A)\)

\(\,\,\,\,\, l=4w, \, A=100\)

\(\,\,\,\,\, \left(4w\right)\left(w\right)=100\)

\(\,\,\,\,\, 4w^2=100\)

\(\,\,\,\,\, w^2=25\)

\(\,\,\,\,\, w=5\)

\(\,\,\,\,\, l=4(w)=4(5)=20\)

\(\,\,\,\,\, \text{Width} = 5 \text{ ft}, \text{Length} = 20 \text{ ft} \)

\(\textbf{3)}\) The length of a rectangular plot is 5 ft more than its width. The area of the plot is 66 square ft. Find the dimensions of the plot.

Show Answer

\( \text{Width} = 6 \text{ ft}, \text{Length} = 11 \text{ ft} \)

Show Work

\(\,\,\,\,\, \text{Length } (l) \, \times \, \text{Width } (w) = \text{Area } (A)\)

\(\,\,\,\,\, l=w+5, \, A=66\)

\(\,\,\,\,\, (w+5)w=66\)

\(\,\,\,\,\, w^2+5w-66=0\)

\(\,\,\,\,\, (w+11)(w-6)=0\)

\(\,\,\,\,\, w=-11 \text{ or } w=6\)

\(\,\,\,\,\, l=6+5=11 \text{ or } l=-11+5=-6\)

\(\,\,\,\,\, \text{Width} = 6 \text{ ft}, \text{Length} = 11 \text{ ft} \)

\(\textbf{4)}\) The length of a rectangle is 15 feet less than its width. The area of the rectangle is 126 square feet. Find the dimensions of the rectangle.

Show Answer

\( \text{Width} = 6 \text{ ft}, \text{Length} = 21 \text{ ft} \)

Show Work

\(\,\,\,\,\, \text{Length } (l) \, \times \, \text{Width } (w) = \text{Area } (A)\)

\(\,\,\,\,\, l=w-15, \, A=126\)

\(\,\,\,\,\, (w-15)w=126\)

\(\,\,\,\,\, w^2-15w-126=0\)

\(\,\,\,\,\, (w-21)(w+6)=0\)

\(\,\,\,\,\, w=21 \text{ or } w=-6\)

\(\,\,\,\,\, l=21-15=6 \text{ or } l=-6-15=-21\)

\(\,\,\,\,\, \text{Width} = 21 \text{ ft}, \text{Length} = 6 \text{ ft} \)

\(\textbf{5)}\) The length of a rectangle is 3 inches more than double the width. The area of the rectangle is 230 square inches. Find the dimensions of the rectangle.

Show Answer

\(\text{Length} = 23 \text{ in}, \text{Width} = 10 \text{ in} \)

Show Work

\(\,\,\,\,\, \text{Length } (l) \, \times \, \text{Width } (w) = \text{Area } (A)\)

\(\,\,\,\,\, l=2w+3, \, A=230\)

\(\,\,\,\,\, (2w+3)w=230\)

\(\,\,\,\,\, 2w^2+3w-230=0\)

\(\,\,\,\,\, (2w+23)(w-10)=0\)

\(\,\,\,\,\, w=-23/2 \text{ or } w=10\)

\(\,\,\,\,\, l=2(10)+3=23 \text{ or } l=2(-23/2)+3=-23+3=-20\)

\(\,\,\,\,\, \text{Length} = 23 \text{ in}, \text{Width} = 10 \text{ in} \)

\(\textbf{6)}\) The length of a rectangle is 5 meters more than triple the width. The area is 138 square meters. Find the dimensions of the rectangle.

Show Answer

\(\text{Width} = 6 \text{ m}, \text{Length} = 23 \text{ m}\)

Show Work

\(\,\,\,\,\, \text{Length } (l) \, \times \, \text{Width } (w) = \text{Area } (A)\)

\(\,\,\,\,\, l=3w+5, \, A=138\)

\(\,\,\,\,\, (3w+5)w=138\)

\(\,\,\,\,\, 3w^2+5w-138=0\)

\(\,\,\,\,\, (3w+23)(w-6)=0\)

\(\,\,\,\,\, w=-23/3 \text{ or } w=6\)

\(\,\,\,\,\, l=3(6)+5=18+5=23 \text{ or } l=3(-23/3)+5=-23+5=-18\)

\(\,\,\,\,\, \text{Width} = 6 \text{ m}, \text{Length} = 23 \text{ m}\)

\(\textbf{7)}\) The width of a rectangle is 6 meters less than its length. The area is 72 square meters. Find the dimensions of the rectangle.

Show Answer

The answer is \( W = 6, L = 12 \)

Show Work

\(\,\,\,\,\, \text{Length } (L) \, \times \, \text{Width } (W) = \text{Area } (A)\)

\(\,\,\,\,\, L = W + 6, \, A = 72\)

\(\,\,\,\,\, (W + 6)W = 72\)

\(\,\,\,\,\, W^2 + 6W – 72 = 0\)

\(\,\,\,\,\, (W + 12)(W – 6) = 0\)

\(\,\,\,\,\, W = -12 \text{ or } W = 6\)

\(\,\,\,\,\, L = 6 + 6 = 12 \text{ or } L = -12 + 6 = -6\)

\(\,\,\,\,\, \text{Width} = 6 \text{ meters}, \text{Length} = 12 \text{ meters} \)

\(\textbf{8)}\) The length of a rectangle is twice the width. The area is 32 square inches. Find the dimensions of the rectangle.

Show Answer

The answer is \( W=4, L=8 \)

Show Work

\(\,\,\,\,\, \text{Length } (L) \, \times \, \text{Width } (W) = \text{Area } (A)\)

\(\,\,\,\,\, L = 2W, \, A = 32\)

\(\,\,\,\,\, (2W)W = 32\)

\(\,\,\,\,\, 2W^2 = 32\)

\(\,\,\,\,\, W^2 = 16\)

\(\,\,\,\,\, W = 4\)

\(\,\,\,\,\, L = 2(4) = 8\)

\(\,\,\,\,\, \text{Width} = 4 \text{ inches}, \text{Length} = 8 \text{ inches} \)

\(\textbf{9)}\) The length of a rectangle is 1 foot less than twice the width. The area is 120 square feet. Find the dimensions of the rectangle.

Show Answer

The answer is \( W = 8, L = 15 \)

Show Work

\(\,\,\,\,\, \text{Length } (L) \, \times \, \text{Width } (W) = \text{Area } (A)\)

\(\,\,\,\,\, L = 2W – 1, \, A = 120\)

\(\,\,\,\,\, (2W – 1)W = 120\)

\(\,\,\,\,\, 2W^2 – W – 120 = 0\)

\(\,\,\,\,\, (2W + 15)(W – 8) = 0\)

\(\,\,\,\,\, W = -15/2 \text{ or } W = 8\)

\(\,\,\,\,\, L = 2(8) – 1 = 16 – 1 = 15 \text{ or } L = 2(-15/2) – 1 = -15 – 1 = -16\)

\(\,\,\,\,\, \text{Width} = 8 \text{ feet}, \text{Length} = 15 \text{ feet} \)

\(\textbf{10)}\) The product of two positive consecutive integers is 56. Find the integers.

Show Answer

The integers are \( 7, 8 \)

Show Work

Let’s call the first integer “n” and the second integer “n + 1”.

\(\,\,\,\,\, n(n + 1) = 56\)

\(\,\,\,\,\, n^2 + n – 56 = 0\)

\(\,\,\,\,\, (n + 8)(n – 7) = 0\)

\(\,\,\,\,\, n = -8 \text{ or } n = 7\)

Since we’re looking for positive integers, the integers are \(7, 8\)

\(\textbf{11)}\) The product of two positive consecutive odd integers is 99. Find the integers.

Show Answer

The integers are \( 9, 11 \)

Show Work

Let’s call the first odd integer “n” and the second odd integer “n + 2”.

\(\,\,\,\,\, n(n + 2) = 99\)

\(\,\,\,\,\, n^2 + 2n – 99 = 0\)

\(\,\,\,\,\, (n + 11)(n – 9) = 0\)

\(\,\,\,\,\, n = -11 \text{ or } n = 9\)

Since we’re looking for positive odd integers, the integers are \(9, 11\)

\(\textbf{12)}\) The product of two positive consecutive odd integers is 1 less than 3 times their sum. Find the integers.

Show Answer

The integers are \( 5, 7 \)

Show Work

Let’s call the first odd integer “n” and the second odd integer “n + 2”.

\(\,\,\,\,\, n(n + 2) = 3(n + n + 2) – 1\)

\(\,\,\,\,\, n^2 + 2n = 6n + 6 – 1\)

\(\,\,\,\,\, n^2 – 4n – 5 = 0\)

\(\,\,\,\,\, (n – 5)(n + 1) = 0\)

\(\,\,\,\,\, n = 5 \text{ or } n = -1\)

Since we’re looking for positive odd integers, the integers are \(5, 7\)

\(\textbf{13)}\) The product of two positive consecutive integers is thirteen less than five times their sum. Find the integers.

Show Answer

The answer is \( 8, 9 \)

Show Work

Let’s call the first integer “n” and the second integer “n + 1”.

\(\,\,\,\,\, n(n + 1) = 5(n + n + 1) – 13\)

\(\,\,\,\,\, n^2 + n = 10n + 5 – 13\)

\(\,\,\,\,\, n^2 – 9n – 8 = 0\)

\(\,\,\,\,\, (n – 8)(n + 1) = 0\)

\(\,\,\,\,\, n = 8 \text{ or } n = -1\)

Since we’re looking for positive integers, the integers are \(8, 9\)

\(\textbf{14)}\) The product of two positive consecutive odd integers is 77 more than twice the larger. Find the integers.

Show Answer

The integers are \( 9, 11 \)

Show Work

Let’s call the first odd integer “n” and the second odd integer “n + 2”.

\(\,\,\,\,\, n(n + 2) = 2(n + 2) + 77\)

\(\,\,\,\,\, n^2 + 2n = 2n + 4 + 77\)

\(\,\,\,\,\, n^2 – 75 = 0\)

\(\,\,\,\,\, (n – 5)(n + 5) = 0\)

\(\,\,\,\,\, n = 5 \text{ or } n = -5\)

Since we’re looking for positive odd integers, the integers are \(5, 7\)

Challenge Problem

\(\textbf{15)}\) The width is twice the height. If the perimeter is 120, what is the area?

Show Area

The area is \( 800\) units\(^2 \)

See Related Pages\(\)

\(\bullet\text{ Adding and Subtracting Polynomials}\)
\(\,\,\,\,\,\,\,\,(4d+7)−(2d−5)…\)

\(\bullet\text{ Multiplying Polynomials}\)
\(\,\,\,\,\,\,\,\,(x+2)(x^2+3x−5)…\)

\(\bullet\text{ Dividing Polynomials}\)
\(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\)

\(\bullet\text{ Dividing Polynomials (Synthetic Division)}\)
\(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\)

\(\bullet\text{ Synthetic Substitution}\)
\(\,\,\,\,\,\,\,\,f(x)=4x^4−3x^2+8x−2…\)

\(\bullet\text{ End Behavior}\)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow \infty, \quad f(x)\rightarrow \infty \)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow -\infty, \quad f(x)\rightarrow \infty… \)

\(\bullet\text{ Completing the Square}\)
\(\,\,\,\,\,\,\,\,x^2+10x−24=0…\)

\(\bullet\text{ Quadratic Formula and the Discriminant}\)
\(\,\,\,\,\,\,\,\,x=-b \pm \displaystyle\frac{\sqrt{b^2-4ac}}{2a}…\)

\(\bullet\text{ Complex Numbers}\)
\(\,\,\,\,\,\,\,\,i=\sqrt{-1}…\)

\(\bullet\text{ Multiplicity of Roots}\)
\(\,\,\,\,\,\,\,\,\)\(…\)

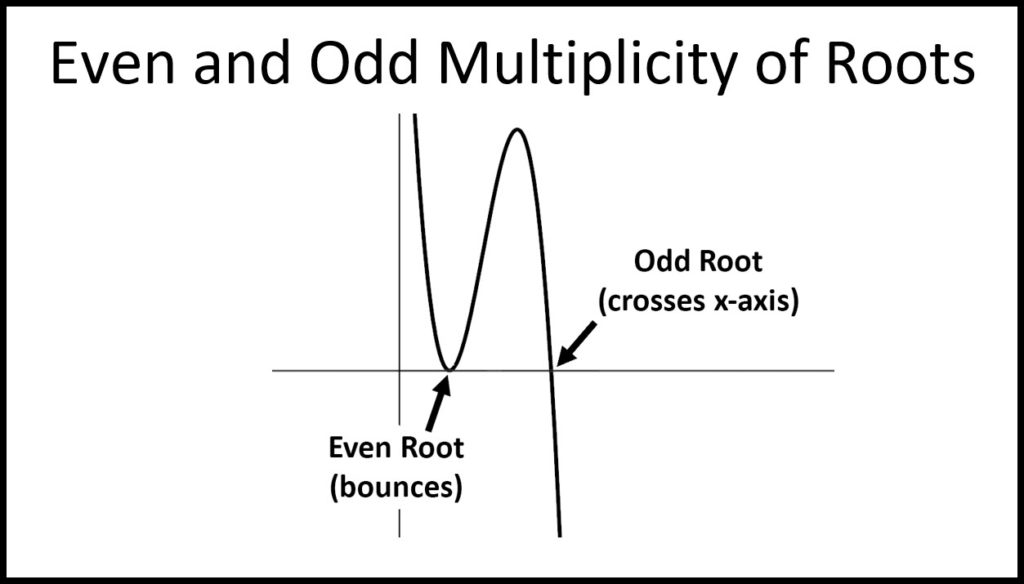\(\bullet\text{ Rational Zero Theorem}\)
\(\,\,\,\,\,\,\,\, \pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 12…\)

\(\bullet\text{ Descartes Rule of Signs}\)
\(\,\)

\(\bullet\text{ Roots and Zeroes}\)
\(\,\,\,\,\,\,\,\,\text{Solve for }x. 3x^2+4x=0…\)

\(\bullet\text{ Linear Factored Form}\)
\(\,\,\,\,\,\,\,\,f(x)=(x+4)(x+1)(x−3)…\)

\(\bullet\text{ Polynomial Inequalities}\)
\(\,\,\,\,\,\,\,\,x^3-4x^2-4x+16 \gt 0…\)

In Summary

Doing quadratic word problems is a great way to reinforce the algebra behind quadratic equations. It also adds a fun element by demonstrating real-world applications.

About Andymath.com

Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.

Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.

Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!

Thank you for visiting. How exciting!