Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
\(\textbf{1)}\) \(\hspace{1ex} (5n^2+3n-2)+(4n^2-5n+3) \)

\(\textbf{2)}\) \(\hspace{1ex} (4d+7)-(2d-5) \)

\(\textbf{3)}\) \(\hspace{1ex} (3xy+4x+2y)-(5xy+5y) \)

\(\textbf{4)}\) \(\hspace{1ex} (3x^2+4x-2)-(5x+5) \)
\(\textbf{5)}\) \(\hspace{1ex} (3x^2+4x+2)+(5x^2-2) \)
\(\textbf{6)}\) \(\hspace{1ex} (x^3+4x^2+2)-(5x^2-2) \)
\(\textbf{7)}\) \(\hspace{1ex} (5x^2-5)-(2x^2-3x^3) \)
\(\textbf{8)}\) \(\hspace{1ex} (7+2x^3)+(5x^3+2) \)
\(\textbf{9)}\) \(\hspace{1ex} (3x^2+1)-(4+4x^2) \)
\(\textbf{10)}\) \(\hspace{1ex} (5x+4)-(5x+1) \)
\(\textbf{11)}\) \(\hspace{1ex} (-4x^4+14+5x^2)+(-3x^4-14x^2-8) \)
\(\textbf{12)}\) \(\hspace{1ex} (12x^5-6x-10x^3)-(9x-2x^5-14x^4) \)
\(\textbf{13)}\) \(\hspace{1ex} (13x^2+11x-2x^4)+(-13x^2-5x-6x^4) \)
\(\textbf{14)}\) \(\hspace{1ex} (8-13x^3-11x)-(2x^3+8-4x^5) \)
\(\textbf{15)}\) \(\hspace{1ex} (2x^5+8x^3-10x^2)-(-12x^5+4x^3=14x^2) \)
\(\textbf{16)}\) \(\hspace{1ex} (8x^4-3-3x^3)+(-5x^4+6x^3-8x^5) \)
\(\textbf{17)}\) \(\hspace{1ex} (6x^2+7x^3)-(-6x^2-7x^3-4x)-(10x+9x^2) \)
\(\textbf{18)}\) \(\hspace{1ex} (-5x^3+7x)+(-5x^3-8x+8x^2)+(-8x^4+8x^3) \)
\(\textbf{19)}\) \(\hspace{1ex} (9y^2-9x^3y^2)+(3y^2+7y^3-8x^3y^3)+(3x^3y^2+2y^2) \)
\(\textbf{20)}\) \(\hspace{1ex} (8y-7x^2y^2)+(-10x^2y+6y+4x^2y^2)-(x^2y+6x^2y^2) \)
See Related Pages\(\)
\(\bullet \text{ Add & Subtract Polynomials Calculator (Symbolab)}\)
\(\bullet\text{ Multiply Monomials}\)
\(\,\,\,\,\,\,\,\,(7m^2 k^5 )(8m^3 k^4 )…\)
\(\bullet\text{ Dividing Monomials}\)
\(\,\,\,\,\,\,\,\,\displaystyle \frac{12x^4 y^3 z}{3x^2 z^4 x}…\)
\(\bullet\text{ Adding and Subtracting Polynomials}\)
\(\,\,\,\,\,\,\,\,(4d+7)−(2d−5)…\)
\(\bullet\text{ Multiplying Polynomials}\)
\(\,\,\,\,\,\,\,\,(x+2)(x^2+3x−5)…\)
\(\bullet\text{ Dividing Polynomials}\)
\(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\)
\(\bullet\text{ Dividing Polynomials (Synthetic Division)}\)
\(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\)
\(\bullet\text{ Synthetic Substitution}\)
\(\,\,\,\,\,\,\,\,f(x)=4x^4−3x^2+8x−2…\)
\(\bullet\text{ End Behavior}\)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow \infty, \quad f(x)\rightarrow \infty \)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow -\infty, \quad f(x)\rightarrow \infty… \)
\(\bullet\text{ Completing the Square}\)
\(\,\,\,\,\,\,\,\,x^2+10x−24=0…\)
\(\bullet\text{ Quadratic Formula and the Discriminant}\)
\(\,\,\,\,\,\,\,\,x=-b \pm \displaystyle\frac{\sqrt{b^2-4ac}}{2a}…\)
\(\bullet\text{ Complex Numbers}\)
\(\,\,\,\,\,\,\,\,i=\sqrt{-1}…\)
\(\bullet\text{ Multiplicity of Roots}\)
\(\,\,\,\,\,\,\,\,\)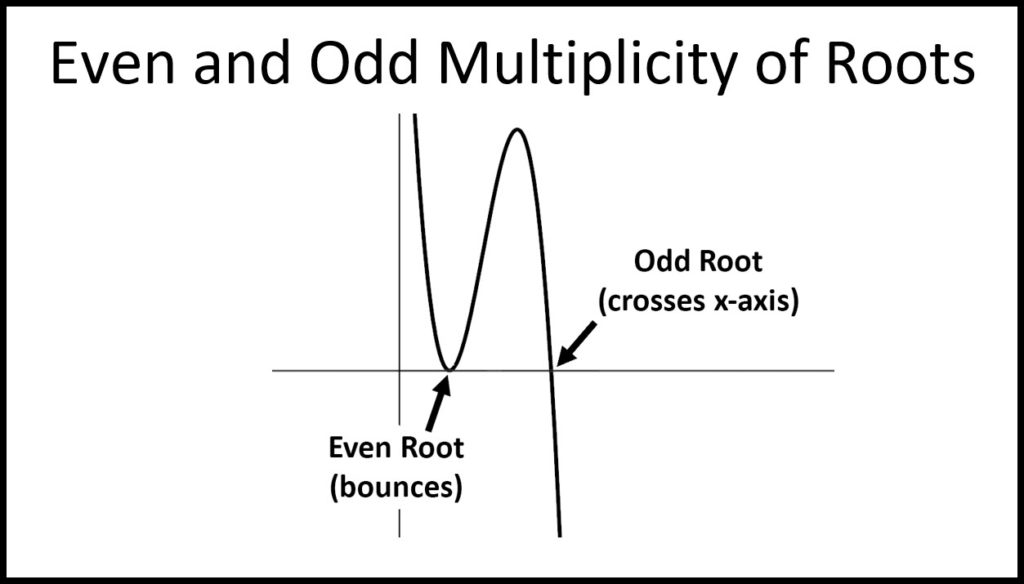 \(…\)
\(…\)
\(\bullet\text{ Rational Zero Theorem}\)
\(\,\,\,\,\,\,\,\, \pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 12…\)
\(\bullet\text{ Descartes Rule of Signs}\)
\(\,\)
\(\bullet\text{ Roots and Zeroes}\)
\(\,\,\,\,\,\,\,\,\text{Solve for }x. 3x^2+4x=0…\)
\(\bullet\text{ Linear Factored Form}\)
\(\,\,\,\,\,\,\,\,f(x)=(x+4)(x+1)(x−3)…\)
\(\bullet\text{ Polynomial Inequalities}\)
\(\,\,\,\,\,\,\,\,x^3-4x^2-4x+16 \gt 0…\)
In Summary
A polynomial is a mathematical expression that is made up of one or more terms, each of which is a variable (or a combination of variables) raised to a non-negative integer power. Polynomials can have constants, called coefficients, in front of the variables, and they can also have a constant term, which is a number that is not associated with any variable. The term “polynomial” comes from the Greek word “poly” meaning “many” and “nomial” meaning “term,” so a polynomial is a mathematical expression with many terms.
Adding and subtracting polynomials involves combining two or more algebraic expressions that consist of multiple terms. This process involves combining like terms by adding or subtracting their coefficients, and simplifying the resulting expression as necessary. Adding and subtracting polynomials is typically taught in an algebra class. Students learn the basics of working with polynomials, including adding, subtracting, multiplying, and dividing them. These skills are essential for success in higher level math classes, such as geometry, trigonometry, and calculus. Polynomials are used in a variety of real world contexts, including engineering, science, and finance.
The most common mistake occurs with subtracting polynomials. The subtraction needs to be distributed to all the terms in the second polynomial.
In the real world, adding and subtracting polynomials is used in a variety of contexts, including engineering, science, and finance. For example, engineers may use polynomials to model complex systems or to solve equations that describe the behavior of a structure or machine. Scientists may use polynomials to represent data or to make predictions about the behavior of a system. In finance, polynomials can be used to model the growth of an investment or the value of a stock over time. Additionally, polynomials can be used in many other fields, such as geography, psychology, and biology, to represent and analyze data and to solve problems. Overall, the ability to work with polynomials is an important skill that can have many practical applications in the real world.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!