Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Notes
Problems & Videos
\(\textbf{1)}\) Simplify \( \displaystyle\sqrt{ }\overline{-24} \)
\(\textbf{2)}\) Simplify \( \sqrt{-6}\cdot \sqrt{-15} \)
\(\textbf{3)}\) Simplify \( -2\sqrt{-18} \cdot 5\sqrt{-8} \)
\(\textbf{4)}\) Simplify \( \sqrt{-48a^6 b^5} \)
\(\textbf{5)}\) Simplify \( i^{33} \)
\(\textbf{6)}\) Simplify \( i^{32} \)
\(\textbf{7)}\) Simplify \( i^{31} \)
\(\textbf{8)}\) Simplify \( (6+4i)+(3-2i) \)
\(\textbf{9)}\) Simplify \( (5-3i)-(3+2i) \)
\(\textbf{10)}\) Simplify \( \displaystyle\frac{2i}{3+4i} \)
\(\textbf{11)}\) Simplify \( \displaystyle\frac{3-2i}{4i} \)
\(\textbf{12)}\) Simplify \( \displaystyle\frac{6+i}{3+2i} \)
\(\textbf{13)}\) Simplify \( (5+i)(5-i) \)
\(\textbf{14)}\) Simplify \( (4+3i)(5-6i) \)
\(\textbf{15)}\) Solve for x, \( 5x^2+125=0 \)
\(\textbf{16)}\) Solve for x and y, \( 4x+2+(y-6)i=10+3i \)
\(\textbf{17)}\) Solve for x and y, \( 5x-12+(3-2y)i=x+7i \)
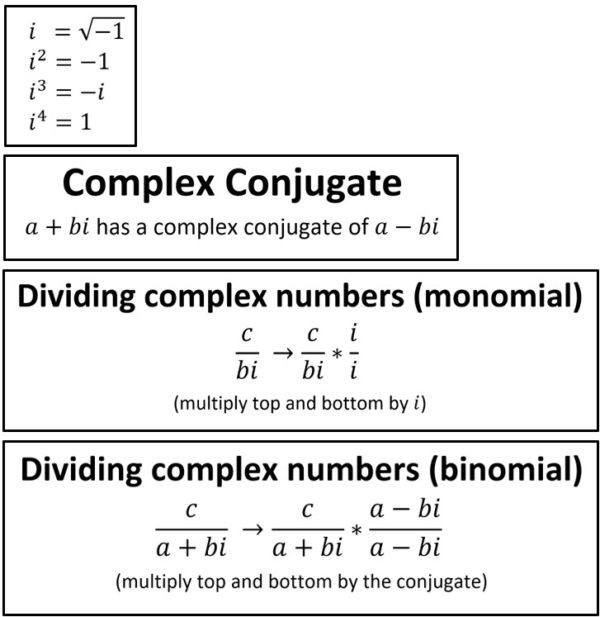
\(\textbf{18)}\) Find the complex conjugate of \( 3+2i \)
\(\textbf{19)}\) Find the complex conjugate of \( 4-5i \)
\(\textbf{20)}\) What is \( 1+i^2 ? \)
\(\textbf{21)}\) What is \( (a+bi)(a-bi)? \)
\(\textbf{22)}\) What is \( (1+\sqrt{-1})(1-\sqrt{-1}) ? \)
\(\textbf{23)}\) Write the standard form of the complex number \(\, 2\left(\cos{60^{\circ}}+i \sin{60^{\circ}}\right) \)
\(\textbf{24)}\) Write the standard form of the complex number \(\, \sqrt{12}\left(\cos{-30^{\circ}}+i \sin{-30^{\circ}}\right) \)
\(\textbf{25)}\) Write the standard form of the complex number \(\, 8\left(\cos{0^{\circ}}+i \sin{0^{\circ}}\right) \)
\(\textbf{26)}\) Simplify \(i^4\)
\(\textbf{27)}\) Simplify \(i^{420}\)
See Related Pages\(\)
\(\bullet\text{ Complex Number Multiplication Visualization on Graph} \)
\(\,\,\,\,\,\,\,\,\text{(Geogebra.org)}\)
\(\bullet\text{ Adding and Subtracting Polynomials}\)
\(\,\,\,\,\,\,\,\,(4d+7)−(2d−5)…\)
\(\bullet\text{ Multiplying Polynomials}\)
\(\,\,\,\,\,\,\,\,(x+2)(x^2+3x−5)…\)
\(\bullet\text{ Dividing Polynomials}\)
\(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\)
\(\bullet\text{ Dividing Polynomials (Synthetic Division)}\)
\(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\)
\(\bullet\text{ Synthetic Substitution}\)
\(\,\,\,\,\,\,\,\,f(x)=4x^4−3x^2+8x−2…\)
\(\bullet\text{ End Behavior}\)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow \infty, \quad f(x)\rightarrow \infty \)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow -\infty, \quad f(x)\rightarrow \infty… \)
\(\bullet\text{ Completing the Square}\)
\(\,\,\,\,\,\,\,\,x^2+10x−24=0…\)
\(\bullet\text{ Quadratic Formula and the Discriminant}\)
\(\,\,\,\,\,\,\,\,x=-b \pm \displaystyle\frac{\sqrt{b^2-4ac}}{2a}…\)
\(\bullet\text{ Complex Numbers}\)
\(\,\,\,\,\,\,\,\,i=\sqrt{-1}…\)
\(\bullet\text{ Multiplicity of Roots}\)
\(\,\,\,\,\,\,\,\,\)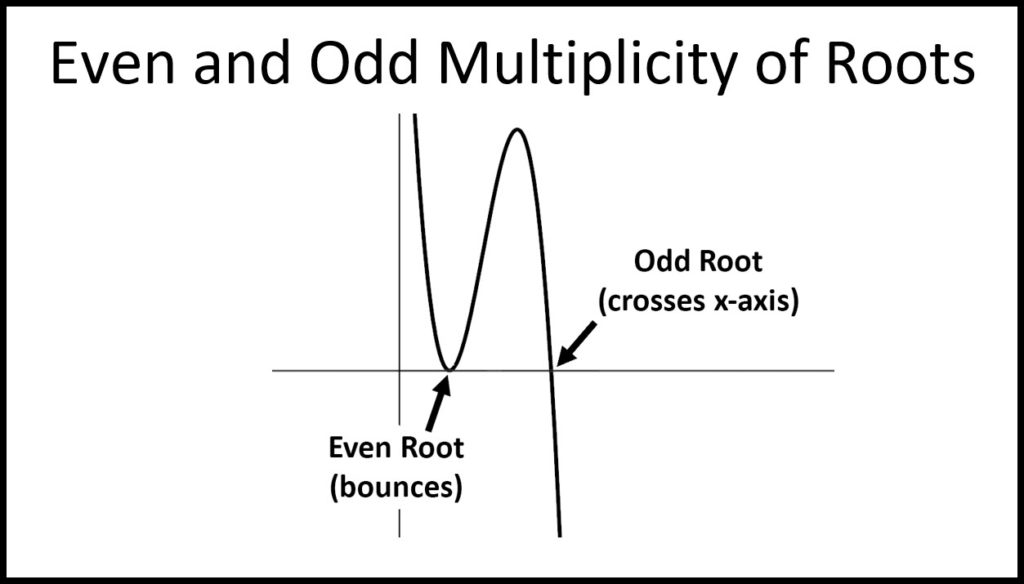 \(…\)
\(…\)
\(\bullet\text{ Rational Zero Theorem}\)
\(\,\,\,\,\,\,\,\, \pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 12…\)
\(\bullet\text{ Descartes Rule of Signs}\)
\(\,\)
\(\bullet\text{ Roots and Zeroes}\)
\(\,\,\,\,\,\,\,\,\text{Solve for }x. 3x^2+4x=0…\)
\(\bullet\text{ Linear Factored Form}\)
\(\,\,\,\,\,\,\,\,f(x)=(x+4)(x+1)(x−3)…\)
\(\bullet\text{ Polynomial Inequalities}\)
\(\,\,\,\,\,\,\,\,x^3-4x^2-4x+16 \gt 0…\)
\(\bullet\text{ Andymath Homepage}\)
In Summary
A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit, which is defined as the square root of -1. Complex numbers extend the concept of a number from the real numbers to the complex plane, which is a two-dimensional plane where the x-axis represents the real part of a complex number and the y-axis represents the imaginary part.
Complex numbers are typically used in a high school algebra or precalculus course, or in a college-level math course such as abstract algebra or complex analysis. They are used in a wide range of fields, including engineering, physics, and computer science.
Complex numbers can be used to represent points in the plane, rotations in space, and even three-dimensional rotations. It is fun and useful to visualize complex numbers on a plane. The real part of the complex number is represented on the x-axis and the imaginary part is represented on the y-axis. We can use this to plot points corresponding to coomplex numbers, and understand how complex numbers behave under various operations. For example, a complex number of the form a + bi can be thought of as a point in the plane with coordinates (a, b).
Complex numbers have many real-world applications in fields such as engineering, physics, and computer science. In electrical engineering, complex numbers are used to represent alternating current (AC) and to analyze circuits with sinusoidal signals. In physics, complex numbers are used to describe the behavior of waves and to solve problems involving harmonic oscillators. In computer science, complex numbers are used in computational geometry, computer graphics, and signal processing.
Overall, complex numbers are a powerful mathematical tool that have many practical applications in the real world.
Topics related to Complex Numbers
Real numbers: Complex numbers are an extension of the real numbers, which are numbers that can be represented on the number line.
Complex plane: The complex plane is a two-dimensional plane where the x-axis represents the real part of a complex number and the y-axis represents the imaginary part.
Complex conjugates: The complex conjugate of a+bi is a – bi. It is obtained by leaving the real part alone and negating the imaginary part of a complex number.
Modulus and argument: The modulus of a complex number is the distance of the number from the origin in the complex plane, and the argument is the angle between the positive x-axis and the line connecting the origin to the number.
Operations on complex numbers: Complex numbers can be added, subtracted, multiplied, and divided using the rules of complex arithmetic.
De Moivre’s theorem: De Moivre’s theorem is a fundamental result in complex analysis that relates complex numbers, their powers, and trigonometric functions.
Quaternions: Quaternions are a generalization of complex numbers to four dimensions, and are used to represent three-dimensional rotations.
Complex analysis: Complex analysis is a branch of mathematics that studies complex functions and their properties using the tools of calculus and algebra. It has many applications in physics, engineering, and other fields.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!