Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Notes
Practice Problems
Divide using synthetic division.
\(\textbf{1)}\) \( \displaystyle\frac{2x^4+4x^2+6x+1}{x+3} \)
\(\textbf{2)}\) \( (x^3-1)(x-1)^{-1} \)
\(\textbf{3)}\) \( \displaystyle\frac{x^3+3x^2-4x+1}{x+3} \)
\(\textbf{4)}\) \( \displaystyle\frac{x^3+3x^2-4x-6}{x+1} \)
\(\textbf{5)}\) \( \displaystyle\frac{x^4+2x^2-3x+7}{x-2} \)
\(\textbf{6)}\) \( \displaystyle\frac{x^5+3x^2-x+1}{x+3} \)
\(\textbf{7)}\) \( \displaystyle\frac{x^3+5x^2+7x+2}{x+2} \)
\(\textbf{8)}\) \( \displaystyle\frac{x^6+x^5+x^2+9x+8}{x+1} \)
See Related Pages\(\)
\(\bullet\text{ Multiply Monomials}\)
\(\,\,\,\,\,\,\,\,(7m^2 k^5 )(8m^3 k^4 )…\)
\(\bullet\text{ Dividing Monomials}\)
\(\,\,\,\,\,\,\,\,\displaystyle \frac{12x^4 y^3 z}{3x^2 z^4 x}…\)
\(\bullet\text{ Adding and Subtracting Polynomials}\)
\(\,\,\,\,\,\,\,\,(4d+7)−(2d−5)…\)
\(\bullet\text{ Multiplying Polynomials}\)
\(\,\,\,\,\,\,\,\,(x+2)(x^2+3x−5)…\)
\(\bullet\text{ Dividing Polynomials}\)
\(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\)
\(\bullet\text{ Synthetic Substitution}\)
\(\,\,\,\,\,\,\,\,f(x)=4x^4−3x^2+8x−2…\)
\(\bullet\text{ End Behavior}\)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow \infty, \quad f(x)\rightarrow \infty \)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow -\infty, \quad f(x)\rightarrow \infty… \)
\(\bullet\text{ Completing the Square}\)
\(\,\,\,\,\,\,\,\,x^2+10x−24=0…\)
\(\bullet\text{ Quadratic Formula and the Discriminant}\)
\(\,\,\,\,\,\,\,\,x=-b \pm \displaystyle\frac{\sqrt{b^2-4ac}}{2a}…\)
\(\bullet\text{ Complex Numbers}\)
\(\,\,\,\,\,\,\,\,i=\sqrt{-1}…\)
\(\bullet\text{ Multiplicity of Roots}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
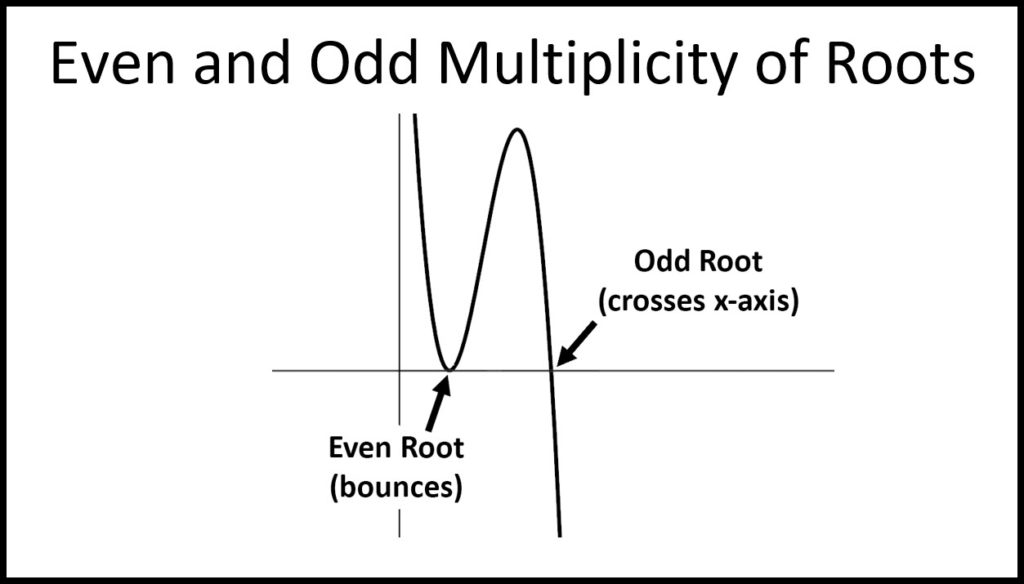\(\bullet\text{ Rational Zero Theorem}\)
\(\,\,\,\,\,\,\,\, \pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 12…\)
\(\bullet\text{ Descartes Rule of Signs}\)
\(\,\)
\(\bullet\text{ Roots and Zeroes}\)
\(\,\,\,\,\,\,\,\,\text{Solve for }x. 3x^2+4x=0…\)
\(\bullet\text{ Linear Factored Form}\)
\(\,\,\,\,\,\,\,\,f(x)=(x+4)(x+1)(x−3)…\)
\(\bullet\text{ Polynomial Inequalities}\)
\(\,\,\,\,\,\,\,\,x^3-4x^2-4x+16 \gt 0…\)
In Summary
Dividing polynomials using synthetic division involves dividing algebraic expressions that consist of multiple terms. This process is similar to polynomial long division, but involves a different set of steps and rules. In synthetic division, the coefficients and variables of each term are divided in a specific order, and the resulting expression is simplified as necessary.
Synthetic division is typically taught in an algebra class. These courses are typically taken by students in high school, although some students may take them earlier or later depending on their individual circumstances. In an algebra class, students learn the basics of working with polynomials, including adding, subtracting, multiplying, and dividing. These skills are essential for success in higher level math classes, such as geometry, trigonometry, and calculus. Synthetic division is a variant of the more general concept of dividing polynomials, and is one of several methods that students may learn in order to divide polynomials.
The most common mistake with synthetic division is to forget to put in “0” place holders if a term is missing. For example \(4x^4+2x^2+x-1\) has coefficients \(4, 0, 2, 1, -1\). Another common mistake is to not put the correct value in the upper left corner. If the factor you are testing is \((x+3)\), you need to put a “-3” in the upper left corner. Practicing a lot of synthetic division problems should help you remember how to do these 2 things correctly.
Related topics related to to synthetic division include factoring, simplifying algebraic expressions, and solving equations. In order to divide polynomials using synthetic division, students must first understand how to factor and simplify algebraic expressions. This involves breaking down a complex expression into simpler parts, and combining like terms to reduce the expression to its simplest form. Additionally, students must be familiar with the order of operations, which determines the sequence in which operations should be performed when evaluating an expression. Solving equations is another related topic, as students may need to solve equations involving polynomials in order to find the value of a variable or to determine the behavior of a system. Overall, synthetic division is a fundamental concept in algebra, and is closely related to many other topics in mathematics.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!