Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Lesson
Notes
Polynomial Examples
\(f(x)=2x^3+3x^2+x-2\)
\(f(x)=2x^6+3x^5+x\)
Not Polynomials
\(f(x)=\displaystyle \frac{3}{x}+5x^{3}+2x+4\)
\(f(x)=5x^{-3}+2x+4\)
\(f(x)=5x^2+\sqrt{x}\)
Practice Problems
Are the following expressions polyomials?
\(\textbf{1)}\) \( 4x^3+2x-3 \)
\(\textbf{2)}\) \( 3x^2+5x-12 \)
\(\textbf{3)}\) \( \displaystyle\frac{2}{x}-7x \)
\(\textbf{4)}\) \( 3xy^2-x+4y^2+x-2 \)
\(5)\) \( \sqrt{x}+\sqrt{y} \)
\(\textbf{6)}\) \(2x+3\)
\(\textbf{7)}\) \(xy^{-3}+3x\)
\(\textbf{8)}\) \(\displaystyle \frac{3}{x}+2\)
\(\textbf{9)}\) \(\displaystyle \frac{x}{3}+2\)
\(\textbf{10)}\) \(5+y^5-7x^4\)
\(\textbf{11)}\) \(\displaystyle \frac{x^2}{3}+\frac{2}{5}\)
\(\textbf{12)}\) \(4xy+2y^3+17\)
\(\textbf{13)}\) \(\sqrt{3}\, x^2+1\)
\(\textbf{14)}\) \(\sqrt{y}\,x^2+5x-1\)
\(\textbf{15)}\) \(\pi+5x\)
\(\textbf{16)}\) \(-3x^4+7\)
See Related Pages\(\)
\(\bullet\text{ Multiply Monomials}\)
\(\,\,\,\,\,\,\,\,(7m^2 k^5 )(8m^3 k^4 )…\)
\(\bullet\text{ Dividing Monomials}\)
\(\,\,\,\,\,\,\,\,\displaystyle \frac{12x^4 y^3 z}{3x^2 z^4 x}…\)
\(\bullet\text{ Adding and Subtracting Polynomials}\)
\(\,\,\,\,\,\,\,\,(4d+7)−(2d−5)…\)
\(\bullet\text{ Multiplying Polynomials}\)
\(\,\,\,\,\,\,\,\,(x+2)(x^2+3x−5)…\)
\(\bullet\text{ Dividing Polynomials}\)
\(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\)
\(\bullet\text{ Dividing Polynomials (Synthetic Division)}\)
\(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\)
\(\bullet\text{ Synthetic Substitution}\)
\(\,\,\,\,\,\,\,\,f(x)=4x^4−3x^2+8x−2…\)
\(\bullet\text{ End Behavior}\)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow \infty, \quad f(x)\rightarrow \infty \)
\(\,\,\,\,\,\,\,\, \text{As } x\rightarrow -\infty, \quad f(x)\rightarrow \infty… \)
\(\bullet\text{ Completing the Square}\)
\(\,\,\,\,\,\,\,\,x^2+10x−24=0…\)
\(\bullet\text{ Quadratic Formula and the Discriminant}\)
\(\,\,\,\,\,\,\,\,x=-b \pm \displaystyle\frac{\sqrt{b^2-4ac}}{2a}…\)
\(\bullet\text{ Complex Numbers}\)
\(\,\,\,\,\,\,\,\,i=\sqrt{-1}…\)
\(\bullet\text{ Multiplicity of Roots}\)
\(\,\,\,\,\,\,\,\,\)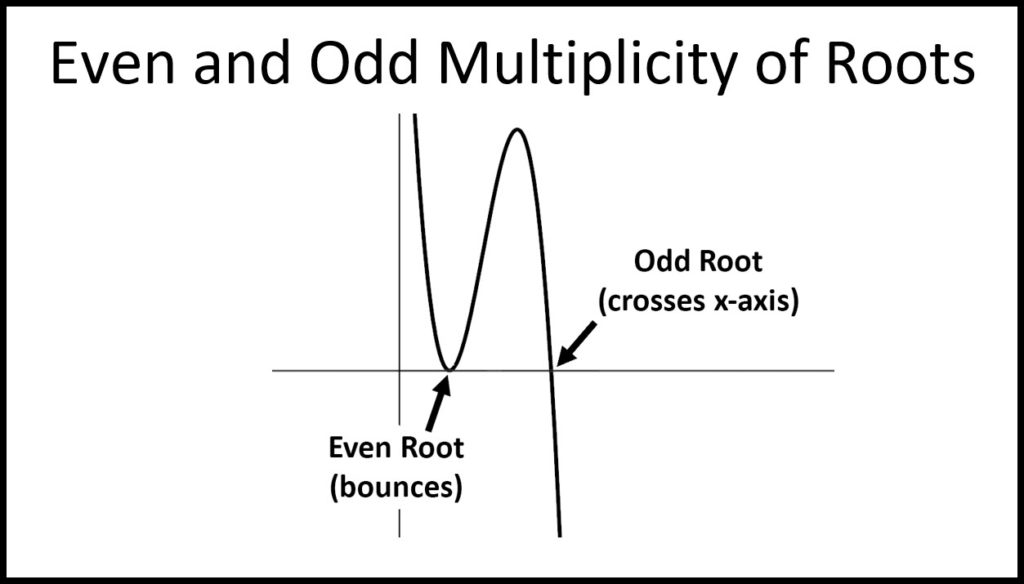 \(…\)
\(…\)
\(\bullet\text{ Rational Zero Theorem}\)
\(\,\,\,\,\,\,\,\, \pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 12…\)
\(\bullet\text{ Descartes Rule of Signs}\)
\(\,\)
\(\bullet\text{ Roots and Zeroes}\)
\(\,\,\,\,\,\,\,\,\text{Solve for }x. 3x^2+4x=0…\)
\(\bullet\text{ Linear Factored Form}\)
\(\,\,\,\,\,\,\,\,f(x)=(x+4)(x+1)(x−3)…\)
\(\bullet\text{ Polynomial Inequalities}\)
\(\,\,\,\,\,\,\,\,x^3-4x^2-4x+16 \gt 0…\)
In Summary
A polynomial is a mathematical expression that is made up of one or more terms, each of which is a variable (or a combination of variables) raised to a non-negative integer power. Polynomials can have constants, called coefficients, in front of the variables, and they can also have a constant term, which is a number that is not associated with any variable. The term “polynomial” comes from the Greek word “poly” meaning “many” and “nomial” meaning “term,” so a polynomial is a mathematical expression with many terms.
Polynomials are typically introduced in algebra classes, which are usually taken in middle or high school. In algebra, students learn about the properties of polynomials and how to manipulate them in equations and expressions. The concept of polynomials is also important in many higher-level math courses, such as calculus, linear algebra, and abstract algebra. Polynomials are also used in many real-world applications, such as in computer science, engineering, and economics.
The concept of polynomials has a long history, dating back to ancient civilizations such as the Babylonians and the Egyptians. However, the modern notion of a polynomial as a mathematical expression made up of terms with variables raised to non-negative integer powers was developed by European mathematicians in the 16th and 17th centuries. The term “polynomial” itself was coined by the French mathematician Albert Girard in 1629. Girard and other mathematicians of his time, such as René Descartes and Pierre de Fermat, made important contributions to the study of polynomials, including the development of techniques for manipulating and solving polynomial equations. The study of polynomials continues to be an active area of research in mathematics, with many new results and applications being discovered today.
There are several topics that are related to polynomials, including algebra, calculus, and number theory. Overall, polynomials are a fundamental and important concept in many different branches of mathematics.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!