Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?

Notes

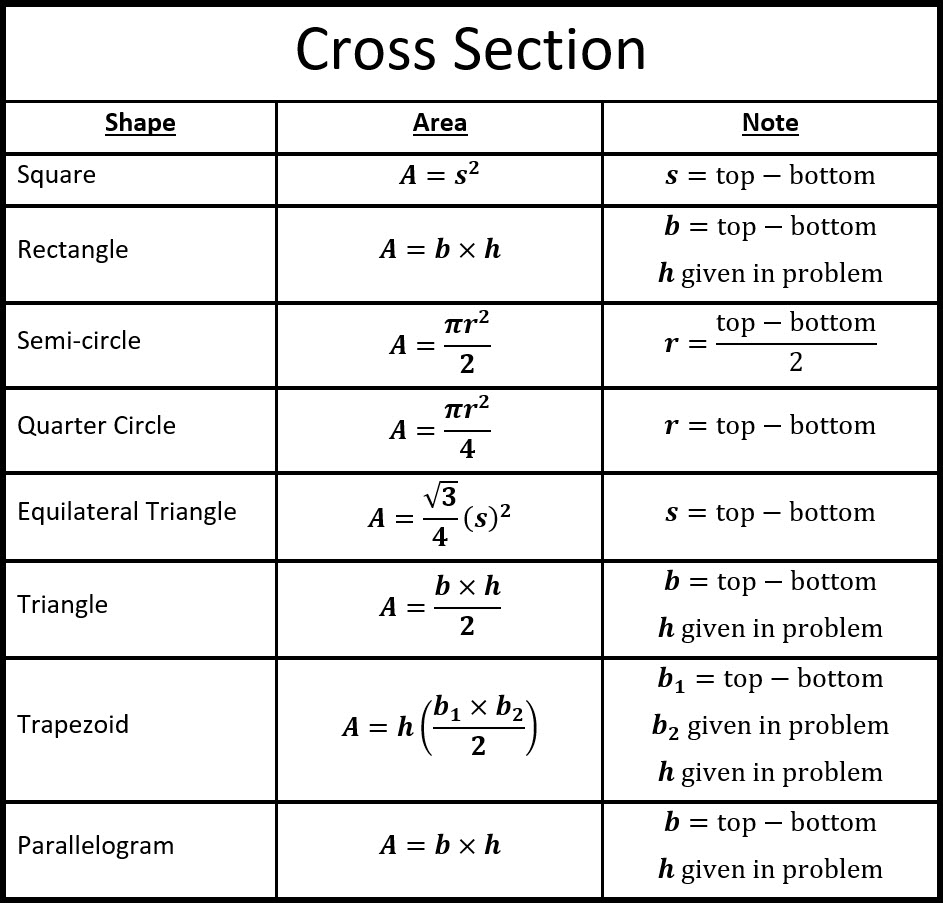
Practice Problems

\(\textbf{1)}\) Find the volume of the solid whose base is the region between \(f(x)=x^2+4\) and \(g(x)=\frac{1}{2}x+1\) from \(x=0\) to \(x=2\) and cross sections taken perpendicular to the x-axis are squares.

Show Volume

Volume\(=31\frac{1}{15} = 31.0\overline{6}\)

Show Work

\(\,\,\,\,\,\,\text{Volume}=\displaystyle \int_{a}^{b}\left(\text{Area}\right) \, dx\)

\(\,\,\,\,\,\,\text{Area of Square}=s^2=\left(f(x)-g(x)\right)^2\)

\(\,\,\,\,\,\,\displaystyle \int_{0}^{2}\left( x^2+4-\left(\frac{1}{2}x+1\right)\right)^2 dx\)

\(\,\,\,\,\,\,\displaystyle \int_{0}^{2}\left( x^2+4-\frac{1}{2}x-1\right)^2 dx\)

\(\,\,\,\,\,\,\displaystyle \int_{0}^{2}\left( x^2-\frac{1}{2}x+3\right)^2 dx\)

\(\,\,\,\,\,\,\displaystyle \int_{0}^{2}\left( x^4-x^3+\frac{25x^2}{4}-3x+9\right) dx\)

\(\,\,\,\,\,\,\displaystyle \left(\frac{x^5}{5}-\frac{x^4}{4}+\frac{25x^3}{12}-\frac{3x^2}{2}+9x\right) \, \big|_0^2\)

\(\,\,\,\,\,\,\displaystyle \left(\frac{(2)^5}{5}-\frac{(2)^4}{4}+\frac{25(2)^3}{12}-\frac{3(2)^2}{2}+9(2)\right)-\left(\frac{(0)^5}{5}-\frac{(0)^4}{4}+\frac{25(0)^3}{12}-\frac{3(0)^2}{2}+9(0)\right)\)

\(\,\,\,\,\,\,\displaystyle \left(\frac{32}{5}-\frac{16}{4}+\frac{200}{12}-\frac{3(4)}{2}+18\right)-\left(0\right)\)

\(\,\,\,\,\,\,\displaystyle \frac{32}{5}-4+\frac{50}{3}-6+18\)

\(\,\,\,\,\,\,\displaystyle \frac{32}{5}-4+\frac{50}{3}-6+18\)

\(\,\,\,\,\,\,\)Volume\(=31\frac{1}{15} = 31.0\overline{6}\)

\(\textbf{2)}\) Find the volume of the solid whose base is the region between \(f(x)=x^2+4\) and \(g(x)=\frac{1}{2}x+1\) from \(x=0\) to \(x=2\) and cross sections taken perpendicular to the x-axis are semi-circles.

Show Volume

Volume\( \approx 12.1999\)

Show Work

\(\,\,\,\,\,\,\text{Volume}=\displaystyle \int_{a}^{b}\left(\text{Area}\right) \, dx\)

\(\,\,\,\,\,\,\text{Area of Semicircle}=\displaystyle\frac{\pi r^2}{2}=\frac{\pi \left(\frac{f(x)-g(x)}{2}\right)^2}{2}\)

\(\,\,\,\,\,\)Volume\(=\displaystyle \int_{0}^{2} \frac{1}{8} \left( x^2+4-\left(\frac{1}{2}x+1\right)\right)^2 \pi \, dx \approx 12.1999\)

\(\textbf{3)}\) Find the volume of the solid whose base is the region between \(f(x)=x^2+4\) and \(g(x)=\frac{1}{2}x+1\) from \(x=0\) to \(x=2\) and cross sections taken perpendicular to the x-axis are equilateral triangles.

Show Volume

Volume\(\approx 13.4523\)

Show Work

\(\,\,\,\,\,\,\text{Volume}=\displaystyle \int_{a}^{b}\left(\text{Area}\right) \, dx\)

\(\,\,\,\,\,\,\)Volume\(=\displaystyle \int_{0}^{2} \frac{1}{4} \left( x^2+4-\left(\frac{1}{2}x+1\right)\right)^2 \sqrt{3} \, dx\approx 13.4523\)

\(\textbf{4)}\) Find the volume of the solid whose base is the region between \(f(x)=\sqrt{x}\) and \(g(x)=x\) from \(x=0\) to \(x=1\) and cross sections taken perpendicular to the x-axis are squares.

Show Volume

Volume\(=\displaystyle\frac{1}{30} \approx 0.0333\)

Show Work

\(\,\,\,\,\,\,\text{Volume}=\displaystyle \int_{a}^{b}\left(\text{Area}\right) \, dx\)

\(\,\,\,\,\,\,\)Volume\(=\displaystyle \int_{0}^{1}\left( \sqrt{x}-x \right)^2 dx =\frac{1}{30} \approx 0.0333\)

\(\textbf{5)}\) Find the volume of the solid whose base is the region between \(f(x)=\sqrt{x}\) and \(g(x)=x\) from \(x=0\) to \(x=1\) and cross sections taken perpendicular to the x-axis are semi-circles.

Show Volume

Volume\(=\displaystyle\frac{\pi}{240} \approx 0.0131\)

Show Work

\(\,\,\,\,\,\,\text{Volume}=\displaystyle \int_{a}^{b}\left(\text{Area}\right) \, dx\)

\(\,\,\,\,\,\,\)Volume\(=\displaystyle \int_{0}^{1} \frac{1}{8} \left( \sqrt{x}-x \right)^2 \pi \, dx=\frac{\pi}{240} \approx 0.0131\)

\(\textbf{6)}\) Find the volume of the solid whose base is the region between \(f(x)=\sqrt{x}\) and \(g(x)=x\) from \(x=0\) to \(x=1\) and cross sections taken perpendicular to the x-axis are equilateral triangles.

Show Volume

Volume\(= \displaystyle\frac{1}{40 \sqrt{3}} \approx 0.0144\)

Show Work

\(\,\,\,\,\,\,\text{Volume}=\displaystyle \int_{a}^{b}\left(\text{Area}\right) \, dx\)

\(\,\,\,\,\,\)Volume\(=\displaystyle \int_{0}^{1} \frac{1}{4} \left( \sqrt{x}-x\right)^2 \sqrt{3} \, dx = \frac{1}{40 \sqrt{3}} \approx 0.0144\)

See Related Pages\(\)

\(\bullet\text{ Calculus Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)

\(\bullet\text{ Trapezoidal Rule}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{b-a}{2n}\left[f(a)+2f(x_1)+2f(x_2)+…+2fx_{n-1}+f(b)\right]…\)

\(\bullet\text{ Properties of Integrals}\)
\(\,\,\,\,\,\,\,\,\displaystyle \int_{a}^{b}cf(x) \, dx=c\displaystyle \int_{a}^{b}f(x) \,dx…\)

\(\bullet\text{ Indefinite Integrals- Power Rule}\)
\(\,\,\,\,\,\,\,\,\displaystyle \int x^n \, dx = \displaystyle \frac{x^{n+1}}{n+1}+C…\)

\(\bullet\text{ Indefinite Integrals- Trig Functions}\)
\(\,\,\,\,\,\,\,\,\displaystyle \int \cos{x} \, dx=\sin{x}+C…\)

\(\bullet\text{ Definite Integrals}\)
\(\,\,\,\,\,\,\,\,\displaystyle \int_{5}^{7} x^3 \, dx…\)

\(\bullet\text{ Integration by Substitution}\)
\(\,\,\,\,\,\,\,\,\displaystyle \int (x^2+3)^3(2x) \,dx…\)

\(\bullet\text{ Area of Region Between Two Curves}\)
\(\,\,\,\,\,\,\,\,A=\displaystyle \int_{a}^{b}\left[f(x)-g(x)\right]\,dx…\)

\(\bullet\text{ Arc Length}\)
\(\,\,\,\,\,\,\,\,\displaystyle \int_{a}^{b}\sqrt{1+\left[f'(x)\right]^2} \,dx…\)

\(\bullet\text{ Average Function Value}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{1}{b-a} \int_{a}^{b}f(x) \,dx\)

\(\bullet\text{ Volume by Cross Sections}\)
\(\,\,\,\,\,\,\,\,\)

\(\bullet\text{ Disk Method}\)
\(\,\,\,\,\,\,\,\,V=\displaystyle \int_{a}^{b}\left[f(x)\right]^2\,dx…\)

\(\bullet\text{ Cylindrical Shells}\)
\(\,\,\,\,\,\,\,\,V=2 \pi \displaystyle \int_{a}^{b} y f(y) \, dy…\)

In Summary

Volume by cross sections is a method of calculating the volume of a three-dimensional object by slicing it into thin cross sections and summing the volumes of these slices. This method is commonly used in calculus to find the volume of complex shapes that may not have a simple formula for finding volume. The volume of an object is defined as the integral of the object’s cross sectional area over its entire length. The cross sectional area is the area of the object’s slice at a particular point along its length.

Volume by cross sections is typically covered in a calculus course, specifically in a unit on integration. Some related topics include integration, the Fundamental Theorem of Calculus, and the concept of volume in general.

About Andymath.com

Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.

Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.

Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!

Thank you for visiting. How exciting!