The Law of Sines & Law of Cosines are used to find the missing sides and angles in non-right triangles.
Law of sines is used whenever at least one side and the angle opposite of the side both have known values.
Law of Cosines is used for all other triangles.
Notes
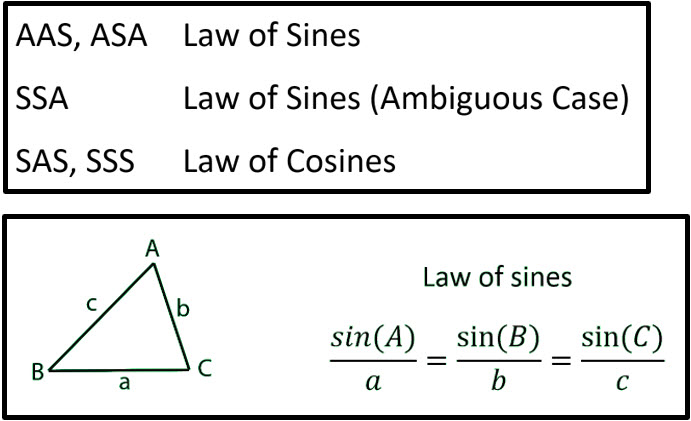
Questions
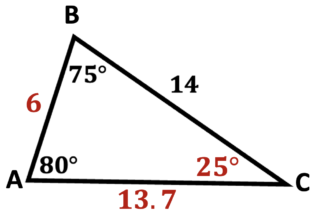
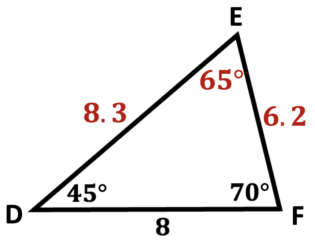
Solve each triangle
\(\textbf{1)}\)
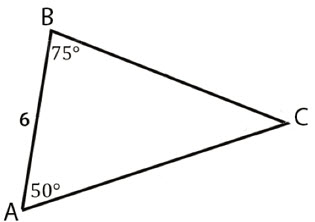
\(\textbf{2)}\)
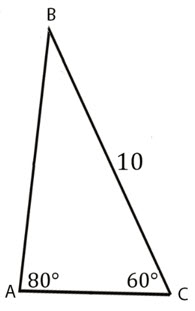
\(\textbf{3)}\)
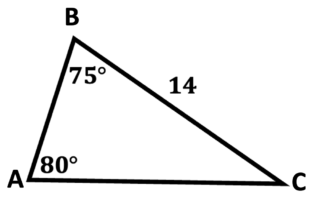
\(\textbf{4)}\)
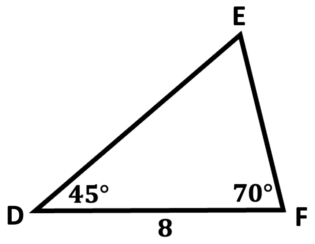
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Triangle Calculator (Calculator.net)}\)
\(\,\,\,\,\,\,\,\,\)
\(\bullet\text{ Right Triangle Trigonometry}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\displaystyle\frac{\text{opp}}{\text{hyp}}…\)
\(\bullet\text{ Angle of Depression and Elevation}\)
\(\,\,\,\,\,\,\,\,\text{Angle of Depression}=\text{Angle of Elevation}…\)
\(\bullet\text{ Convert to Radians and to Degrees}\)
\(\,\,\,\,\,\,\,\,\text{Radians} \rightarrow \text{Degrees}, \times \displaystyle \frac{180^{\circ}}{\pi}…\)
\(\bullet\text{ Degrees, Minutes and Seconds}\)
\(\,\,\,\,\,\,\,\,48^{\circ}34’21”…\)
\(\bullet\text{ Coterminal Angles}\)
\(\,\,\,\,\,\,\,\,\pm 360^{\circ} \text { or } \pm 2\pi n…\)
\(\bullet\text{ Reference Angles}\)
\(\,\,\,\,\,\,\,\,\)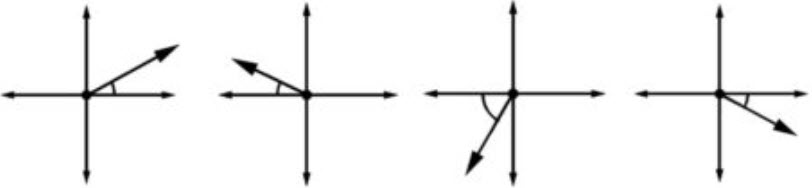 \(…\)
\(…\)
\(\bullet\text{ Find All 6 Trig Functions}\)
\(\,\,\,\,\,\,\,\,\)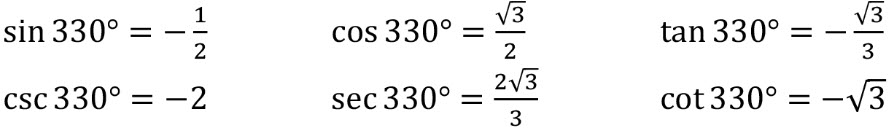 \(…\)
\(…\)
\(\bullet\text{ Unit Circle}\)
\(\,\,\,\,\,\,\,\,\sin{(60^{\circ})}=\displaystyle\frac{\sqrt{3}}{2}…\)
\(\bullet\text{ Law of Sines}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}\) 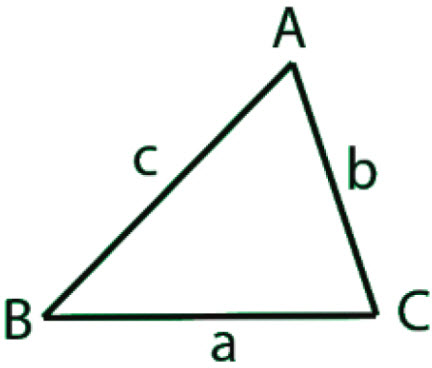 \(…\)
\(…\)
\(\bullet\text{ Area of SAS Triangles}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\frac{1}{2}ab \sin{C}\)  \(…\)
\(…\)
\(\bullet\text{ Law of Cosines}\)
\(\,\,\,\,\,\,\,\,a^2=b^2+c^2-2bc \cos{A}\)  \(…\)
\(…\)
\(\bullet\text{ Area of SSS Triangles (Heron’s formula)}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\sqrt{s(s-a)(s-b)(s-c)}\)  \(…\)
\(…\)
\(\bullet\text{ Geometric Mean}\)
\(\,\,\,\,\,\,\,\,x=\sqrt{ab} \text{ or } \displaystyle\frac{a}{x}=\frac{x}{b}…\)
\(\bullet\text{ Geometric Mean- Similar Right Triangles}\)
\(\,\,\,\,\,\,\,\,\)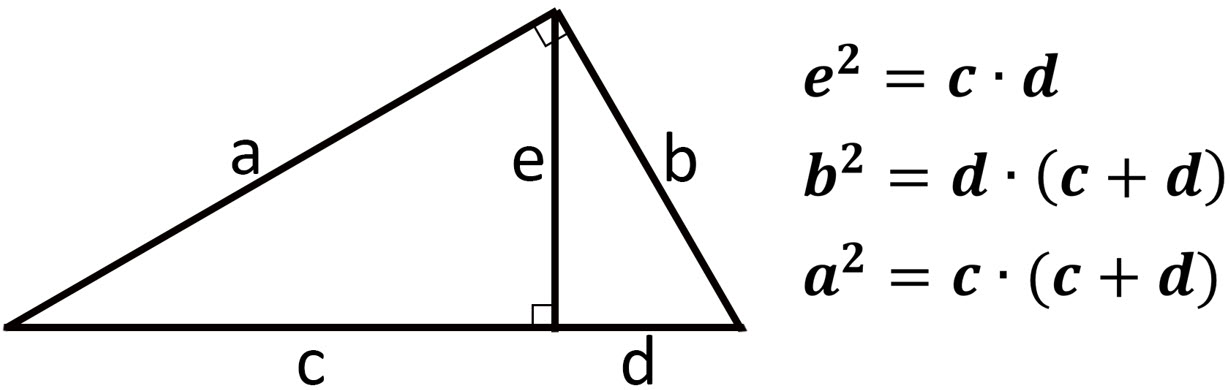 \(…\)
\(…\)
\(\bullet\text{ Inverse Trigonmetric Functions}\)
\(\,\,\,\,\,\,\,\,\sin {\left(cos^{-1}\left(\frac{3}{5}\right)\right)}…\)
\(\bullet\text{ Sum and Difference of Angles Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}…\)
\(\bullet\text{ Double-Angle and Half-Angle Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(2A)}=2\sin{(A)}\cos{(A)}…\)
\(\bullet\text{ Trigonometry-Pythagorean Identities}\)
\(\,\,\,\,\,\,\,\,\sin^2{(x)}+\cos^2{(x)}=1…\)
\(\bullet\text{ Product-Sum Identities}\)
\(\,\,\,\,\,\,\,\,\cos{\alpha}\cos{\beta}=\left(\displaystyle\frac{\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}}{2}\right)…\)
\(\bullet\text{ Cofunction Identities}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\cos{(\frac{\pi}{2}-x)}…\)
\(\bullet\text{ Proving Trigonometric Identities}\)
\(\,\,\,\,\,\,\,\,\sec{x}-\cos{x}=\displaystyle\frac{\tan^2{x}}{\sec{x}}…\)
\(\bullet\text{ Graphing Trig Functions- sin and cos}\)
\(\,\,\,\,\,\,\,\,f(x)=A \sin{B(x-c)}+D \)  \(…\)
\(…\)
\(\bullet\text{ Solving Trigonometric Equations}\)
\(\,\,\,\,\,\,\,\,2\cos{(x)}=\sqrt{3}…\)
\(\bullet\text{ Andymath Homepage}\)
In Summary
The Law of Sines, also known as the sine formula or sine rule, is a mathematical relationship that relates the lengths of the sides of a triangle to the sines of its angles. This important concept is used in trigonometry, which is a branch of mathematics that studies triangles and circles.
The Law of Sines states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all sides and angles in the triangle. This means that if we know two sides and the included angle (SAS) or two angles and a side (AAS) of a triangle, we can use the Law of Sines to find the remaining unknown values.
We learn about the Law of Sines in math classes because it is a useful tool for solving problems involving triangles, specifically non-right triangles.
The Law of Sines is typically taught in high school math classes, such as geometry or trigonometry. It is also a fundamental concept in advanced math courses, such as calculus and differential equations.
The Law of Sines is related to the Law of Cosines. The Law of Cosines is another formula that relates the sides and angles of a triangle and is used to solve problems involving right triangles.
In addition to its use in mathematics, the Law of Sines has practical applications in various fields, such as engineering, physics, and astronomy. It is used to solve problems involving the measurement of distances and angles in three-dimensional space and to determine the shape and size of celestial objects.
Real world examples of Law of Sines
Surveying: The Law of Sines is used in surveying to measure distances and angles between points on the Earth’s surface. Surveyors use a device called a theodolite, which measures angles in two dimensions, to determine the distance and direction to a point. The Law of Sines can be used to calculate the distance to the point using the angle and the known distance from the theodolite to the point.
Navigation: Navigators use the Law of Sines to calculate the distance to a distant object, such as a ship or a lighthouse, by measuring the angle between the object and the horizon. This is known as celestial navigation.
Satellite communication: The Law of Sines is used in satellite communication to calculate the distance between a satellite and a ground station. The satellite transmits a signal to the ground station, which measures the time it takes for the signal to arrive. The Law of Sines can be used to calculate the distance based on the time delay and the angles between the satellite and the ground station.
Astronomy: Astronomers use the Law of Sines to calculate the size and shape of celestial objects, such as planets and stars. By measuring the angles between the object and other points in the sky, and using the known distances between those points, astronomers can determine the distance to the object and its size.
Construction: The Law of Sines is used in construction to calculate the length of a missing side in a triangle. For example, if a contractor needs to build a triangular foundation for a house, but only knows the lengths of two sides and the included angle, they can use the Law of Sines to find the length of the third side. This is especially useful in situations where it is difficult to measure the lengths of all sides directly.
Topics that use Law of Sines
Law of Cosines: The Law of Cosines is another formula that relates the sides and angles of a triangle. It is used to solve problems involving triangles when we know the lengths of all three sides of the triangle, or when we know two sides and the included angle. The Law of Cosines is often used in conjunction with the Law of Sines to solve more complex problems involving triangles.
Spherical trigonometry: Spherical trigonometry is the study of triangles on the surface of a sphere. It is used in fields such as astronomy and geography to calculate distances and angles between points on a sphere. The Law of Sines is a fundamental concept in spherical trigonometry and is used to solve problems involving triangles on a sphere.
Triangulation: Triangulation is a method of finding the location of an object using the principles of geometry and trigonometry. It involves measuring the angles between the object and two known points, and using the Law of Sines to calculate the distance to the object. Triangulation is used in a variety of fields, including surveying, navigation, and telecommunications.
Vector calculus: Vector calculus is a branch of mathematics that deals with vector-valued functions and their derivatives. It is used to analyze and describe physical phenomena, such as fluid flow and electric and magnetic fields. The Law of Sines is used in vector calculus to solve problems involving triangles and vector fields.
Differential equations: Differential equations are equations that describe how a variable changes over time. They are used to model physical systems and predict how they will behave. The Law of Sines is used in the solution of certain types of differential equations, such as those involving triangles and oscillations.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!