Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
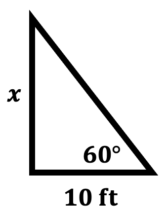
\(\textbf{1)}\) You are standing 10 feet from the base of a tree. You look up at the top of the tree with an angle of elevation of 60 degrees. How tall is the tree?
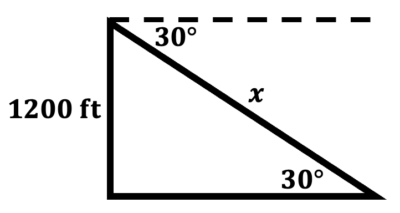
\(\textbf{2)}\) You are in a hot air balloon. You look at Steve with an angle of depression of 30 degrees. Your elevation is 1200 feet. How far apart are you and Steve?
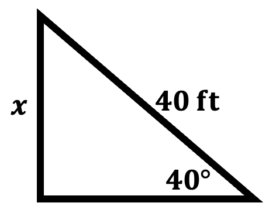
\(\textbf{3)}\) You are flying a kite. You let out 40 feet of string at an angle of elevation of 40 degrees. How high up is the kite?
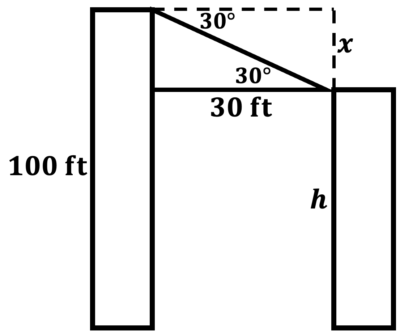
\(\textbf{4)}\) You are on top of a building. You look down on the neighboring building at an angle of depression of 30 degrees. Your building is 100 feet tall. The buildings are 30 feet apart. How tall is the other building?
\(\textbf{5)}\) From the top of a lighthouse, the angle of depression to a boat is 45 degrees. If the lighthouse is 100 feet tall, how far is the boat from the base of the lighthouse?
\(\textbf{6)}\) You are flying a kite and hold the string 80 feet long. The angle of elevation to the kite is 50 degrees. How high is the kite above the ground?
\(\textbf{7)}\) A person looks up at the top of a cliff with an angle of elevation of 20 degrees. If they are standing 200 feet away from the base of the cliff, how tall is the cliff?
\(\textbf{8)}\) From the top of a building, the angle of depression to a car on the street is 40 degrees. If the building is 80 feet tall, how far is the car from the base of the building?
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Right Triangle Trigonometry}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\displaystyle\frac{\text{opp}}{\text{hyp}}…\)
\(\bullet\text{ Angle of Depression and Elevation}\)
\(\,\,\,\,\,\,\,\,\text{Angle of Depression}=\text{Angle of Elevation}…\)
\(\bullet\text{ Convert to Radians and to Degrees}\)
\(\,\,\,\,\,\,\,\,\text{Radians} \rightarrow \text{Degrees}, \times \displaystyle \frac{180^{\circ}}{\pi}…\)
\(\bullet\text{ Degrees, Minutes and Seconds}\)
\(\,\,\,\,\,\,\,\,48^{\circ}34’21”…\)
\(\bullet\text{ Coterminal Angles}\)
\(\,\,\,\,\,\,\,\,\pm 360^{\circ} \text { or } \pm 2\pi n…\)
\(\bullet\text{ Reference Angles}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
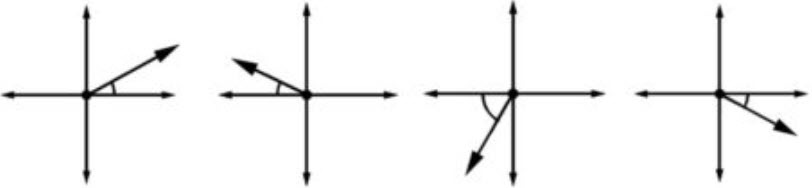\(\bullet\text{ Find All 6 Trig Functions}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
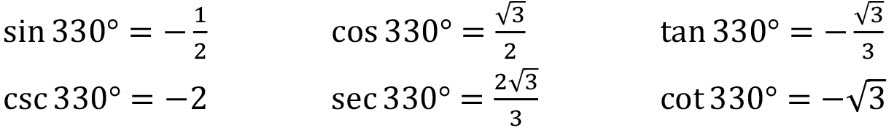\(\bullet\text{ Unit Circle}\)
\(\,\,\,\,\,\,\,\,\sin{(60^{\circ})}=\displaystyle\frac{\sqrt{3}}{2}…\)
\(\bullet\text{ Law of Sines}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}\)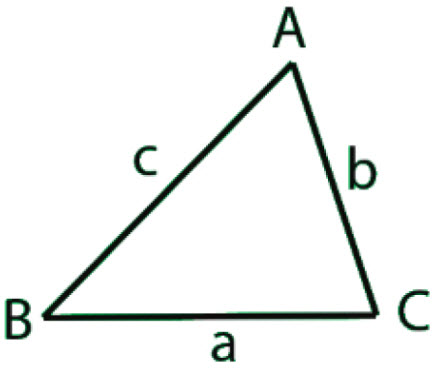 
\(…\)
\(\bullet\text{ Area of SAS Triangles}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\frac{1}{2}ab \sin{C}\) \(…\)
\(\bullet\text{ Law of Cosines}\)
\(\,\,\,\,\,\,\,\,a^2=b^2+c^2-2bc \cos{A}\) \(…\)
\(\bullet\text{ Area of SSS Triangles (Heron’s formula)}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\sqrt{s(s-a)(s-b)(s-c)}\) \(…\)
\(\bullet\text{ Geometric Mean}\)
\(\,\,\,\,\,\,\,\,x=\sqrt{ab} \text{ or } \displaystyle\frac{a}{x}=\frac{x}{b}…\)
\(\bullet\text{ Geometric Mean- Similar Right Triangles}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
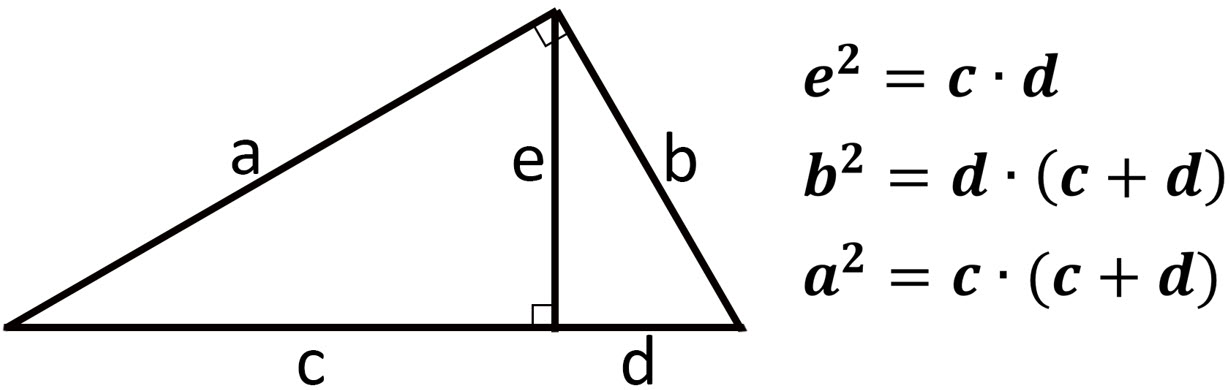\(\bullet\text{ Inverse Trigonmetric Functions}\)
\(\,\,\,\,\,\,\,\,\sin {\left(cos^{-1}\left(\frac{3}{5}\right)\right)}…\)
\(\bullet\text{ Sum and Difference of Angles Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}…\)
\(\bullet\text{ Double-Angle and Half-Angle Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(2A)}=2\sin{(A)}\cos{(A)}…\)
\(\bullet\text{ Trigonometry-Pythagorean Identities}\)
\(\,\,\,\,\,\,\,\,\sin^2{(x)}+\cos^2{(x)}=1…\)
\(\bullet\text{ Product-Sum Identities}\)
\(\,\,\,\,\,\,\,\,\cos{\alpha}\cos{\beta}=\left(\displaystyle\frac{\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}}{2}\right)…\)
\(\bullet\text{ Cofunction Identities}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\cos{(\frac{\pi}{2}-x)}…\)
\(\bullet\text{ Proving Trigonometric Identities}\)
\(\,\,\,\,\,\,\,\,\sec{x}-\cos{x}=\displaystyle\frac{\tan^2{x}}{\sec{x}}…\)
\(\bullet\text{ Graphing Trig Functions- sin and cos}\)
\(\,\,\,\,\,\,\,\,f(x)=A \sin{B(x-c)}+D \) 
\(…\)
\(\bullet\text{ Solving Trigonometric Equations}\)
\(\,\,\,\,\,\,\,\,2\cos{(x)}=\sqrt{3}…\)
In Summary
Word problems in trigonometry often involve finding the angle of depression or elevation. These angles are formed between a horizontal line of sight and a line of sight downward or upward, respectively.
Word problems involving angle of depression and elevation are typically covered in high school trigonometry or precalculus classes. We learn about these because it provides a practical application for the concepts learned in this branch of mathematics. These types of problems can be found in fields such as surveying, meteorology, and navigation.
Common mistakes when solving word problems involving angle of depression and elevation is not understanding which angle is the angle of depression. It is usually not the upper angle in the triangle drawing for the problem. It is the angle off of the horizontal line. Usually the angle of depression is equal to the angle of elevation, which is usually the bottom acute angle in the drawing.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!