The Geometric Mean is a type of average found by multiplying the two numbers together and then taking the square root.
Lesson
Notes
Questions
Find the geometric mean of the following numbers.
\(\textbf{1)}\) Find the geometric mean of \( 4\) and \(9 \)
\(\textbf{2)}\) Find the Geometric Mean of \( 8\) and \(2 \)
\(\textbf{3)}\) Find the Geometric Mean of \( 4\) and \(20 \)
\(\textbf{4)}\) Find the Geometric Mean of \( 3\) and \(10 \)
\(\textbf{5)}\) Find the Geometric Mean of \( 7\) and \(21 \)
\(\textbf{6)}\) Find the Geometric Mean of \( 3\) and \(12 \)
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Right Triangle Trigonometry}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\displaystyle\frac{\text{opp}}{\text{hyp}}…\)
\(\bullet\text{ Angle of Depression and Elevation}\)
\(\,\,\,\,\,\,\,\,\text{Angle of Depression}=\text{Angle of Elevation}…\)
\(\bullet\text{ Convert to Radians and to Degrees}\)
\(\,\,\,\,\,\,\,\,\text{Radians} \rightarrow \text{Degrees}, \times \displaystyle \frac{180^{\circ}}{\pi}…\)
\(\bullet\text{ Degrees, Minutes and Seconds}\)
\(\,\,\,\,\,\,\,\,48^{\circ}34’21”…\)
\(\bullet\text{ Coterminal Angles}\)
\(\,\,\,\,\,\,\,\,\pm 360^{\circ} \text { or } \pm 2\pi n…\)
\(\bullet\text{ Reference Angles}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
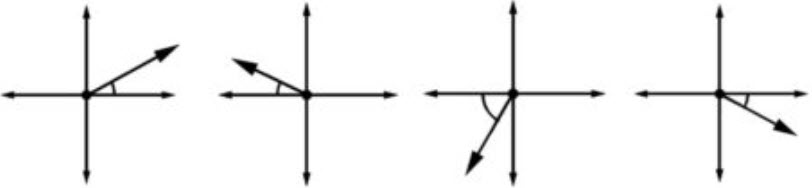\(\bullet\text{ Find All 6 Trig Functions}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
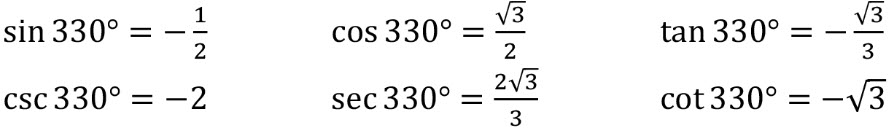\(\bullet\text{ Unit Circle}\)
\(\,\,\,\,\,\,\,\,\sin{(60^{\circ})}=\displaystyle\frac{\sqrt{3}}{2}…\)
\(\bullet\text{ Law of Sines}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}\)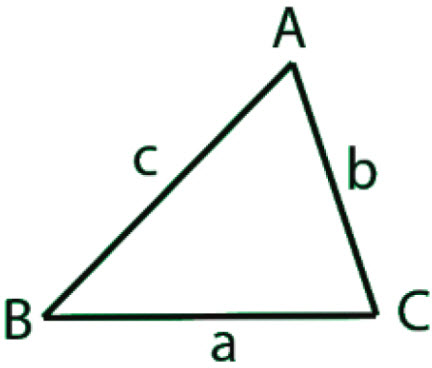 
\(…\)
\(\bullet\text{ Area of SAS Triangles}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\frac{1}{2}ab \sin{C}\) \(…\)
\(\bullet\text{ Law of Cosines}\)
\(\,\,\,\,\,\,\,\,a^2=b^2+c^2-2bc \cos{A}\) \(…\)
\(\bullet\text{ Area of SSS Triangles (Heron’s formula)}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\sqrt{s(s-a)(s-b)(s-c)}\) \(…\)
\(\bullet\text{ Geometric Mean}\)
\(\,\,\,\,\,\,\,\,x=\sqrt{ab} \text{ or } \displaystyle\frac{a}{x}=\frac{x}{b}…\)
\(\bullet\text{ Geometric Mean- Similar Right Triangles}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
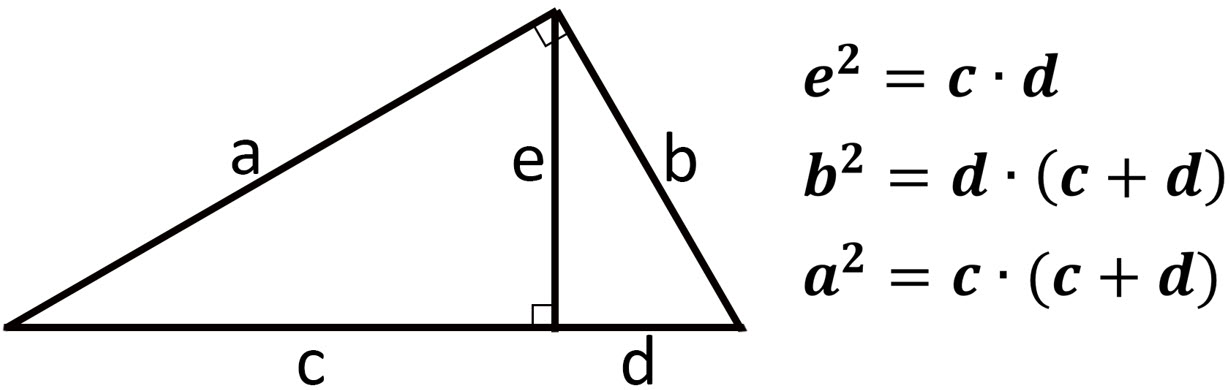\(\bullet\text{ Inverse Trigonmetric Functions}\)
\(\,\,\,\,\,\,\,\,\sin {\left(cos^{-1}\left(\frac{3}{5}\right)\right)}…\)
\(\bullet\text{ Sum and Difference of Angles Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}…\)
\(\bullet\text{ Double-Angle and Half-Angle Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(2A)}=2\sin{(A)}\cos{(A)}…\)
\(\bullet\text{ Trigonometry-Pythagorean Identities}\)
\(\,\,\,\,\,\,\,\,\sin^2{(x)}+\cos^2{(x)}=1…\)
\(\bullet\text{ Product-Sum Identities}\)
\(\,\,\,\,\,\,\,\,\cos{\alpha}\cos{\beta}=\left(\displaystyle\frac{\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}}{2}\right)…\)
\(\bullet\text{ Cofunction Identities}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\cos{(\frac{\pi}{2}-x)}…\)
\(\bullet\text{ Proving Trigonometric Identities}\)
\(\,\,\,\,\,\,\,\,\sec{x}-\cos{x}=\displaystyle\frac{\tan^2{x}}{\sec{x}}…\)
\(\bullet\text{ Graphing Trig Functions- sin and cos}\)
\(\,\,\,\,\,\,\,\,f(x)=A \sin{B(x-c)}+D \) 
\(…\)
\(\bullet\text{ Solving Trigonometric Equations}\)
\(\,\,\,\,\,\,\,\,2\cos{(x)}=\sqrt{3}…\)
\(\bullet\text{ Andymath Homepage}\)
In Summary
The geometric mean is a type of average that is used to compare the relative sizes of two or more numbers. It is calculated by taking the product of the numbers and then taking the nth root of the result, where n is the number of numbers being averaged. The geometric mean is typically smaller than the arithmetic mean, and is often used to compare quantities that are multiplied together, such as rates of growth or rates of decay. The geometric mean is typically introduced in a course on algebra or precalculus, as it is an important concept for understanding the properties of numbers and their relationships to one another.
One common mistake when working with the geometric mean is to confuse it with the arithmetic mean, which is the sum of the numbers divided by the number of numbers being averaged. Another common mistake is to forget to use the appropriate value of n when calculating the geometric mean.
A fun fact about the geometric mean is that it is used in the definition of the golden ratio, which is a number that is considered to be aesthetically pleasing and occurs frequently in nature. The golden ratio is the ratio of the geometric mean of two numbers to the larger of the two numbers.
The geometric mean has many applications in the real world, including comparing rates of growth or decay, calculating compound interest, and determining the average size of a set of numbers.
Some related topics to the geometric mean include algebra, arithmetic mean, and the properties of numbers and their relationships to one another. Other related topics include geometry, trigonometry, and the properties of geometric shapes and their relationships to one another.
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!