Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?

Law of Cosines Proof Video

Notes

Questions

Solve each triangle

\(\textbf{1)}\) Solve the triangle.

Show Answer

\(\angle A\approx73.9^{\circ} \,\,\, \angle B\approx46.1^{\circ} \,\,\, c=\sqrt{13}\approx3.61\)

Show Work

\(\text{Step 1: Find the missing side, side } c\)

\(\,\,\,\,\,\,c^2=a^2+b^2-2ab\cos{C}\)

\(\,\,\,\,\,\,c^2=4^2+3^2-2(4)(3)\cos{60}\)

\(\,\,\,\,\,\,c^2=4^2+3^2-2(4)(3)\cdot \frac{1}{2}\)

\(\,\,\,\,\,\,c^2=16+9-12\)

\(\,\,\,\,\,\,c^2=13\)

\(\,\,\,\,\,\,c=\sqrt{13}\approx 3.61\)

\(\text{Step 2: Find the first missing angle, } \angle B\)

\(\,\,\,\,\,\,\displaystyle\frac{\sin{C}}{c}=\frac{\sin{B}}{b}\)

\(\,\,\,\,\,\,\displaystyle\frac{\sin{60}}{\sqrt{13}}=\frac{\sin{B}}{3}\)

\(\,\,\,\,\,\,\displaystyle \sqrt{13} \cdot \sin{B}=3 \cdot \sin{60}=\)

\(\,\,\,\,\,\,\displaystyle 3.605551 \cdot \sin{B} =3 \cdot .866025\)

\(\,\,\,\,\,\,\displaystyle 3.605551 \cdot \sin{B} =2.59808\)

\(\,\,\,\,\,\,\displaystyle \sin{B} =.720578\)

\(\,\,\,\,\,\,\displaystyle B=\sin^{-1}(.720578)\)

\(\,\,\,\,\,\,\displaystyle \angle B \approx 46.1^{\circ}\)

\(\text{Step 3: Find the last missing angle, } \angle A\)

\(\,\,\,\,\,\,\angle A+\angle B + \angle C = 180\)

\(\,\,\,\,\,\,\angle A+ 46.1 + 60 = 180\)

\(\,\,\,\,\,\,\angle A+ 106.1 = 180\)

\(\,\,\,\,\,\,\displaystyle \angle A \approx 73.9^{\circ}\)

\(\text{The answer is}\angle A\approx73.9^{\circ} \,\,\, \angle B\approx46.1^{\circ} \,\,\, c=\sqrt{13}\approx3.61\)

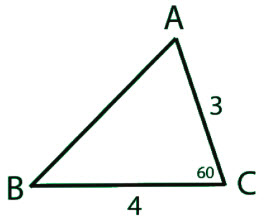
\(\textbf{2)}\) Solve the triangle.

Show Answer

\(\angle A\approx106.6^{\circ} \,\,\, \angle B\approx48.2^{\circ} \,\,\, \angle C\approx25.2^{\circ}\)

Show Work

\(\text{Step 1: Find the largest angle, } \angle A\)

\(\,\,\,\,\,\,a^2=b^2+c^2-2bc\cos{A}\)

\(\,\,\,\,\,\,9^2=7^2+4^2-2(7)(4)\cos{A}\)

\(\,\,\,\,\,\,81=49+16-56\cos{A}\)

\(\,\,\,\,\,\,81=65-56\cos{A}\)

\(\,\,\,\,\,\,16=-56\cos{A}\)

\(\,\,\,\,\,\,-.285714=\cos{A}\)

\(\,\,\,\,\,\,\cos^{-1}(-.285714)=A\)

\(\,\,\,\,\,\,\angle A\approx106.6^{\circ}\)

\(\text{Step 2: Find the second largest angle, } \angle B\)

\(\,\,\,\,\,\,\displaystyle\frac{\sin{A}}{a}=\frac{\sin{B}}{b}\)

\(\,\,\,\,\,\,\displaystyle\frac{\sin{106.6}}{9}=\frac{\sin{B}}{7}\)

\(\,\,\,\,\,\,\displaystyle 9\sin{B}=7\sin{106.6}\)

\(\,\,\,\,\,\,\displaystyle 9\sin{B}=7\cdot .95832\)

\(\,\,\,\,\,\,\displaystyle 9\sin{B}=6.7082\)

\(\,\,\,\,\,\,\displaystyle \sin{B}=.745356\)

\(\,\,\,\,\,\,\displaystyle B=\sin^{-1}(.745356)\)

\(\,\,\,\,\,\,\displaystyle \angle B \approx 48.2^{\circ}\)

\(\text{Step 3: Find the last angle, } \angle C\)

\(\,\,\,\,\,\,\angle A+\angle B + \angle C = 180\)

\(\,\,\,\,\,\,106.6+48.2 + \angle C = 180\)

\(\,\,\,\,\,\,154.8 + \angle C = 180\)

\(\,\,\,\,\,\, \angle C = 25.2^{\circ}\)

\(\text{The answer is }\angle A\approx106.6^{\circ} \,\,\, \angle B\approx48.2^{\circ} \,\,\, \angle C\approx25.2^{\circ}\)

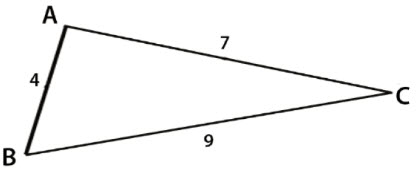
\(\textbf{3)}\) Solve the triangle.

Show Answer

\( \angle C \approx 62.2^{\circ} ,\,\angle E \approx 33.5^{\circ} ,\,\angle J \approx 84.3^{\circ} \)

Show Work

\(\text{Step 1: Find the largest angle, } \angle J\)

\(\,\,\,\,\,\,j^2=c^2+e^2-2ce\cos{J}\)

\(\,\,\,\,\,\,9^2=8^2+5^2-2(8)(5)\cos{J}\)

\(\,\,\,\,\,\,81=64+25-80\cos{J}\)

\(\,\,\,\,\,\,81=89-80\cos{J}\)

\(\,\,\,\,\,\,-8=-80\cos{J}\)

\(\,\,\,\,\,\,0.1=\cos{J}\)

\(\,\,\,\,\,\,\cos^{-1}(0.1)=J\)

\(\,\,\,\,\,\,\angle J\approx84.3^{\circ}\)

\(\text{Step 2: Find the second largest angle, } \angle C\)

\(\,\,\,\,\,\,\displaystyle\frac{\sin{J}}{j}=\frac{\sin{C}}{c}\)

\(\,\,\,\,\,\,\displaystyle\frac{\sin{84.3}}{9}=\frac{\sin{C}}{8}\)

\(\,\,\,\,\,\,\displaystyle 9\sin{C}=8\sin{84.3}\)

\(\,\,\,\,\,\,\displaystyle 9\sin{C}=8\cdot 0.995\)

\(\,\,\,\,\,\,\displaystyle 9\sin{C}=7.9604\)

\(\,\,\,\,\,\,\displaystyle \sin{C}=0.88449\)

\(\,\,\,\,\,\,\displaystyle C=\sin^{-1}(0.88449)\)

\(\,\,\,\,\,\,\displaystyle \angle C \approx 62.2^{\circ}\)

\(\text{Step 3: Find the last angle, } \angle E\)

\(\,\,\,\,\,\,\angle J+\angle C + \angle E = 180\)

\(\,\,\,\,\,\,84.3+62.2 + \angle E = 180\)

\(\,\,\,\,\,\,146.5 + \angle E = 180\)

\(\,\,\,\,\,\, \angle E = 33.5^{\circ}\)

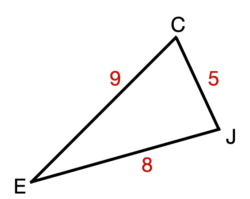
\(\textbf{4)}\) Solve the triangle.

Show Answer

\( \angle B \approx 53.1^{\circ} ,\, \angle M \approx 36.9^{\circ} ,\, \angle T \approx 90^{\circ} \)

Show Work

\(\text{Step 1: Find the largest angle, } \angle T\)

\(\,\,\,\,\,\,t^2=m^2+b^2-2mb\cos{T}\)

\(\,\,\,\,\,\,15^2=9^2+12^2-2(9)(12)\cos{T}\)

\(\,\,\,\,\,\,225=81+144-216\cos{T}\)

\(\,\,\,\,\,\,225=225-216\cos{T}\)

\(\,\,\,\,\,\,-0=-216\cos{T}\)

\(\,\,\,\,\,\,0=\cos{T}\)

\(\,\,\,\,\,\,\cos^{-1}(0)=T\)

\(\,\,\,\,\,\,\angle T=90^{\circ}\)

\(\text{Step 2: Find the second largest angle, } \angle B\)

\(\,\,\,\,\,\,\displaystyle\frac{\sin{T}}{t}=\frac{\sin{B}}{b}\)

\(\,\,\,\,\,\,\displaystyle\frac{\sin{90}}{15}=\frac{\sin{B}}{12}\)

\(\,\,\,\,\,\,\displaystyle 15\sin{B}=12\sin{90}\)

\(\,\,\,\,\,\,\displaystyle 15\sin{B}=12\)

\(\,\,\,\,\,\,\displaystyle \sin{B}=0.8\)

\(\,\,\,\,\,\,\displaystyle B=\sin^{-1}(0.8)\)

\(\,\,\,\,\,\,\displaystyle \angle B \approx 53.1^{\circ}\)

\(\text{Step 3: Find the last angle, } \angle M\)

\(\,\,\,\,\,\,\angle T+\angle B + \angle M = 180\)

\(\,\,\,\,\,\,90+53.1 + \angle M = 180\)

\(\,\,\,\,\,\,143.1 + \angle M = 180\)

\(\,\,\,\,\,\, \angle M = 36.9^{\circ}\)

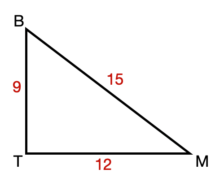
\(\textbf{5)}\) Solve the triangle.

Show Answer

\( \angle D \approx 123^{\circ},\, \angle F \approx 16^{\circ},\, \angle G \approx 41^{\circ} \)

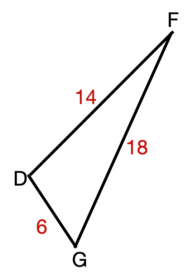
\(\textbf{6)}\) Solve the triangle.

Show Answer

\( \angle A \approx 23^{\circ},\, \angle D \approx 67^{\circ},\, \angle N \approx 90^{\circ} \)

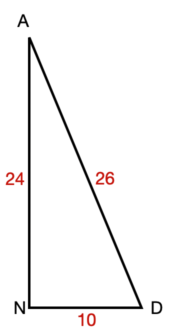
\(\textbf{7)}\) Solve the triangle.

Show Answer

\( a \approx 4.194,\, \angle B \approx 123.01^{\circ}, \, \angle C \approx 33.99^{\circ}\)

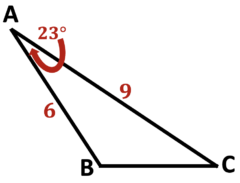
\(\textbf{8)}\) Solve the triangle.

Show Answer

\( a \approx 7.522,\, \angle B \approx 87.99^{\circ}, \, \angle C \approx 22.01^{\circ}\)

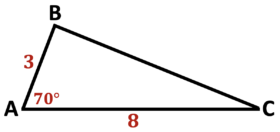
\(\textbf{9)}\) Solve the triangle.

Show Answer

\( c= \sqrt{7} \approx 2.6458,\, \angle A \approx 19.11^{\circ}, \, \angle B \approx 100.89^{\circ} \)

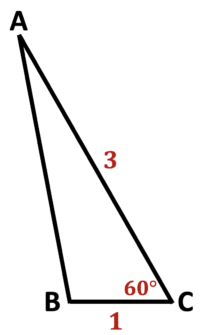
\(\textbf{10)}\) Solve the triangle.

Show Answer

\( b=7,\, \angle A \approx 21.79^{\circ}, \, \angle C \approx 38.21^{\circ} \)

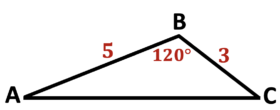
See Related Pages\(\)

\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)

\(\bullet\text{ Triangle Calculator (Calculator.net)}\)
\(\,\,\,\,\,\,\,\,\)

\(\bullet\text{ Right Triangle Trigonometry}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\displaystyle\frac{\text{opp}}{\text{hyp}}…\)

\(\bullet\text{ Angle of Depression and Elevation}\)
\(\,\,\,\,\,\,\,\,\text{Angle of Depression}=\text{Angle of Elevation}…\)

\(\bullet\text{ Convert to Radians and to Degrees}\)
\(\,\,\,\,\,\,\,\,\text{Radians} \rightarrow \text{Degrees}, \times \displaystyle \frac{180^{\circ}}{\pi}…\)

\(\bullet\text{ Degrees, Minutes and Seconds}\)
\(\,\,\,\,\,\,\,\,48^{\circ}34’21”…\)

\(\bullet\text{ Coterminal Angles}\)
\(\,\,\,\,\,\,\,\,\pm 360^{\circ} \text { or } \pm 2\pi n…\)

\(\bullet\text{ Reference Angles}\)
\(\,\,\,\,\,\,\,\,\)\(…\)

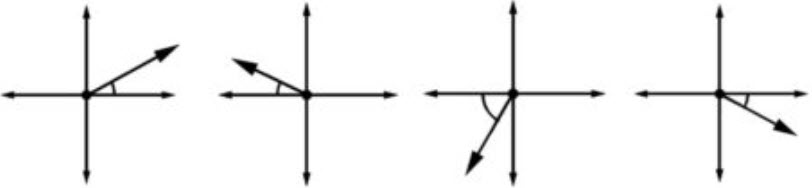\(\bullet\text{ Find All 6 Trig Functions}\)
\(\,\,\,\,\,\,\,\,\)\(…\)

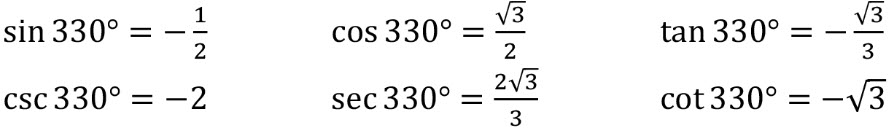\(\bullet\text{ Unit Circle}\)
\(\,\,\,\,\,\,\,\,\sin{(60^{\circ})}=\displaystyle\frac{\sqrt{3}}{2}…\)

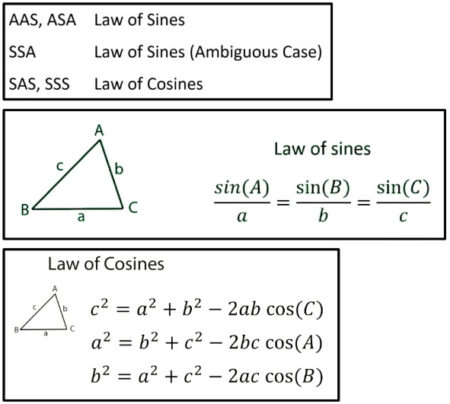
\(\bullet\text{ Law of Sines}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}\) \(…\)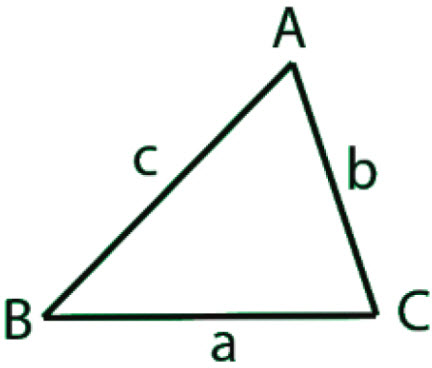

\(\bullet\text{ Area of SAS Triangles}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\frac{1}{2}ab \sin{C}\) \(…\)

\(\bullet\text{ Law of Cosines}\)
\(\,\,\,\,\,\,\,\,a^2=b^2+c^2-2bc \cos{A}\) \(…\)

\(\bullet\text{ Area of SSS Triangles (Heron’s formula)}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\sqrt{s(s-a)(s-b)(s-c)}\) \(…\)

\(\bullet\text{ Geometric Mean}\)
\(\,\,\,\,\,\,\,\,x=\sqrt{ab} \text{ or } \displaystyle\frac{a}{x}=\frac{x}{b}…\)

\(\bullet\text{ Geometric Mean- Similar Right Triangles}\)
\(\,\,\,\,\,\,\,\,\)\(…\)

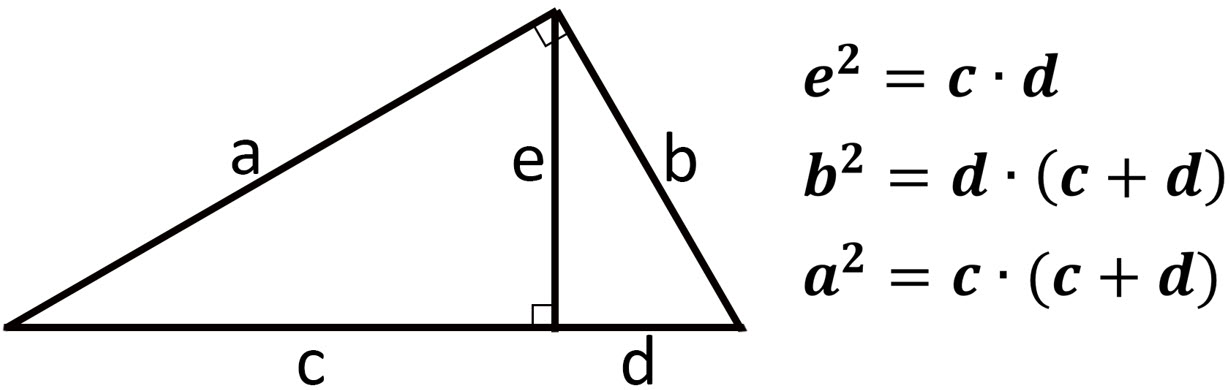\(\bullet\text{ Inverse Trigonmetric Functions}\)
\(\,\,\,\,\,\,\,\,\sin {\left(cos^{-1}\left(\frac{3}{5}\right)\right)}…\)

\(\bullet\text{ Sum and Difference of Angles Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}…\)

\(\bullet\text{ Double-Angle and Half-Angle Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(2A)}=2\sin{(A)}\cos{(A)}…\)

\(\bullet\text{ Trigonometry-Pythagorean Identities}\)
\(\,\,\,\,\,\,\,\,\sin^2{(x)}+\cos^2{(x)}=1…\)

\(\bullet\text{ Product-Sum Identities}\)
\(\,\,\,\,\,\,\,\,\cos{\alpha}\cos{\beta}=\left(\displaystyle\frac{\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}}{2}\right)…\)

\(\bullet\text{ Cofunction Identities}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\cos{(\frac{\pi}{2}-x)}…\)

\(\bullet\text{ Proving Trigonometric Identities}\)
\(\,\,\,\,\,\,\,\,\sec{x}-\cos{x}=\displaystyle\frac{\tan^2{x}}{\sec{x}}…\)

\(\bullet\text{ Graphing Trig Functions- sin and cos}\)
\(\,\,\,\,\,\,\,\,f(x)=A \sin{B(x-c)}+D \) \(…\)

\(\bullet\text{ Solving Trigonometric Equations}\)
\(\,\,\,\,\,\,\,\,2\cos{(x)}=\sqrt{3}…\)

\(\bullet\text{ Andymath Homepage}\)

In Summary

The Law of Cosines is a mathematical formula that relates the lengths of the sides of a triangle to the cosine of one of its angles. It is an important tool for solving problems involving triangles, particularly in geometry and trigonometry.

The Law of Cosines states that in any triangle, the square of the length of one side is equal to the sum of the squares of the lengths of the other two sides minus twice the product of those two sides and the cosine of the angle between them. This can be written as:

\(a^2 = b^2 + c^2 – 2bc \cdot \cos{(A)}\)

We learn about the Law of Cosines because it is a useful tool for solving problems involving triangles. It should be used when you want to solve an unknown side of angles in SAS triangles or SSS triangles.

The Law of Cosines is typically taught in a high school geometry class along with Law of Sines. And these lessons occur around the middle to the end of a entire section on trigonometry.

The most common mistake when using the Law of Cosines is to add the \(b^2 + c^2\) and the \(2bc\) together before multiplying the \(2bc\) by the \(\cos{(A)}\). The correct order of operations multiplies the \(2bc \cdot \cos{(A)}\) and then adding that to \(b^2 + c^2\).

It should be noted that the pythagorean theorem is a specific case of the law of cosines. If the angle between the two sides is 90 degrees, then the \(2bc \cdot \cos{(A)}\) is equal to zero and we end up with simply \(a^2+b^2=c^2\).

Real world examples of Law of Cosines

Finding the distance between two points on a map: The Law of Cosines can be used to find the distance between two points on a map. If you can treat the points as the vertices of an SAS triangle, the distance between the two points can be calculated using the Law of Cosines.

Calculating the height of a building: The Law of Cosines can be used to find the height of a building if enough info is know to create an SAS triangle with the third side being the building.

Measuring the height of a mountain: Same idea as the height of a building, as long as an SAS triangle can be formed with the height of the mountain as the third unknown side, we can use law of cosines to find the height of the building.

About Andymath.com

Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.

Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.

Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!

Thank you for visiting. How exciting!