Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Notes
Problems & Videos
Solve the following right triangles
\(\textbf{1)}\) Find the missing sides and angles.
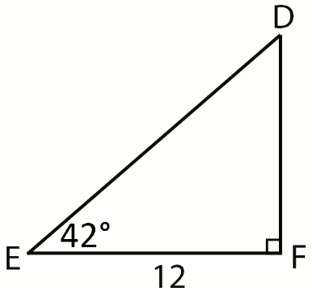

\(\textbf{2)}\) Find the missing sides and angles.
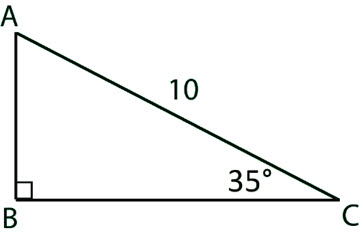
\(\textbf{3)}\) Find the missing sides and angles.
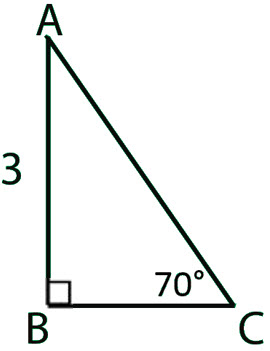
\(\textbf{4)}\) Express \(\cos{32^{\circ}}\) in terms of sine.
\(\textbf{5)}\) Express \(\sin{48^{\circ}}\) in terms of cosine.
See Related Pages\(\)
\(\bullet\text{ Geometry Homepage}\)
\(\,\,\,\,\,\,\,\,\text{All the Best Topics…}\)
\(\bullet\text{ Right Triangle Trigonometry}\)
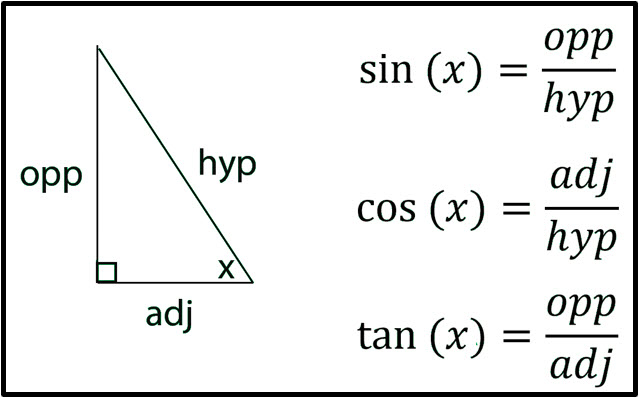
\(\,\,\,\,\,\,\,\,\sin{(x)}=\displaystyle\frac{\text{opp}}{\text{hyp}}…\)
\(\bullet\text{ Angle of Depression and Elevation}\)
\(\,\,\,\,\,\,\,\,\text{Angle of Depression}=\text{Angle of Elevation}…\)
\(\bullet\text{ Convert to Radians and to Degrees}\)
\(\,\,\,\,\,\,\,\,\text{Radians} \rightarrow \text{Degrees}, \times \displaystyle \frac{180^{\circ}}{\pi}…\)
\(\bullet\text{ Degrees, Minutes and Seconds}\)
\(\,\,\,\,\,\,\,\,48^{\circ}34’21”…\)
\(\bullet\text{ Coterminal Angles}\)
\(\,\,\,\,\,\,\,\,\pm 360^{\circ} \text { or } \pm 2\pi n…\)
\(\bullet\text{ Reference Angles}\)
\(\,\,\,\,\,\,\,\,\)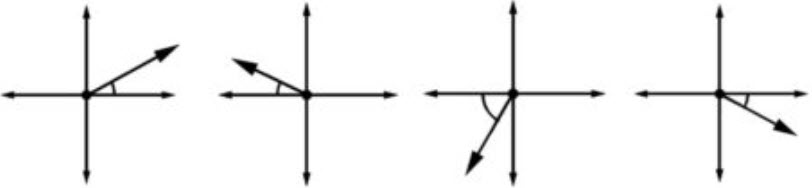 \(…\)
\(…\)
\(\bullet\text{ Find All 6 Trig Functions}\)
\(\,\,\,\,\,\,\,\,\)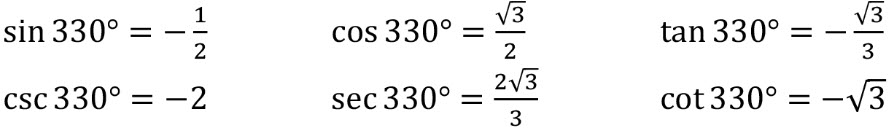 \(…\)
\(…\)
\(\bullet\text{ Unit Circle}\)
\(\,\,\,\,\,\,\,\,\sin{(60^{\circ})}=\displaystyle\frac{\sqrt{3}}{2}…\)
\(\bullet\text{ Law of Sines}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}\) 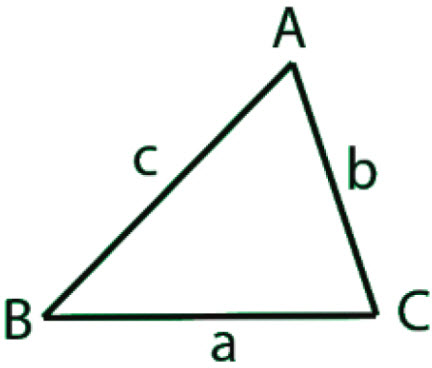 \(…\)
\(…\)
\(\bullet\text{ Area of SAS Triangles}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\frac{1}{2}ab \sin{C}\)  \(…\)
\(…\)
\(\bullet\text{ Law of Cosines}\)
\(\,\,\,\,\,\,\,\,a^2=b^2+c^2-2bc \cos{A}\)  \(…\)
\(…\)
\(\bullet\text{ Area of SSS Triangles (Heron’s formula)}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\sqrt{s(s-a)(s-b)(s-c)}\)  \(…\)
\(…\)
\(\bullet\text{ Geometric Mean}\)
\(\,\,\,\,\,\,\,\,x=\sqrt{ab} \text{ or } \displaystyle\frac{a}{x}=\frac{x}{b}…\)
\(\bullet\text{ Geometric Mean- Similar Right Triangles}\)
\(\,\,\,\,\,\,\,\,\)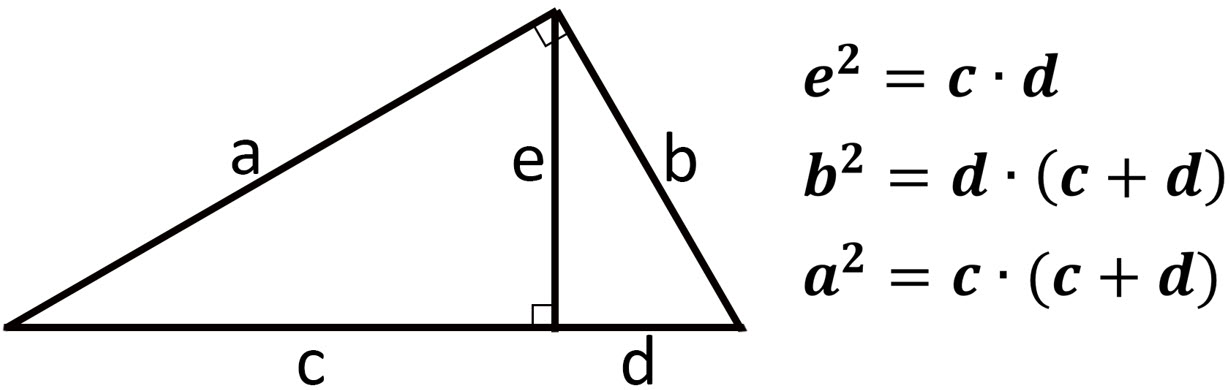 \(…\)
\(…\)
\(\bullet\text{ Inverse Trigonmetric Functions}\)
\(\,\,\,\,\,\,\,\,\sin {\left(cos^{-1}\left(\frac{3}{5}\right)\right)}…\)
\(\bullet\text{ Sum and Difference of Angles Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}…\)
\(\bullet\text{ Double-Angle and Half-Angle Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(2A)}=2\sin{(A)}\cos{(A)}…\)
\(\bullet\text{ Trigonometry-Pythagorean Identities}\)
\(\,\,\,\,\,\,\,\,\sin^2{(x)}+\cos^2{(x)}=1…\)
\(\bullet\text{ Product-Sum Identities}\)
\(\,\,\,\,\,\,\,\,\cos{\alpha}\cos{\beta}=\left(\displaystyle\frac{\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}}{2}\right)…\)
\(\bullet\text{ Cofunction Identities}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\cos{(\frac{\pi}{2}-x)}…\)
\(\bullet\text{ Proving Trigonometric Identities}\)
\(\,\,\,\,\,\,\,\,\sec{x}-\cos{x}=\displaystyle\frac{\tan^2{x}}{\sec{x}}…\)
\(\bullet\text{ Graphing Trig Functions- sin and cos}\)
\(\,\,\,\,\,\,\,\,f(x)=A \sin{B(x-c)}+D \)  \(…\)
\(…\)
\(\bullet\text{ Solving Trigonometric Equations}\)
\(\,\,\,\,\,\,\,\,2\cos{(x)}=\sqrt{3}…\)
In Summary…
Right triangle trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of right triangles. A right triangle is a triangle with one right angle, and the side opposite the right angle is called the hypotenuse. The other two sides are called the legs of the triangle.
The trigonometric functions are used to describe the relationships between the sides and angles of a right triangle. The three main trigonometric functions are sine, cosine, and tangent. These functions are often abbreviated as sin, cos, and tan, respectively.
The sine function is defined as the ratio of the length of the side opposite an angle to the length of the hypotenuse \(\left(\frac{\text{opposite}}{\text{hypotenuse}}\right)\). The cosine function is defined as the ratio of the length of the adjacent side to the length of the hypotenuse \(\left(\frac{\text{adjacent}}{\text{hypotenuse}}\right)\). And the tangent function is defined as the ratio of the length of the opposite side to the length of the adjacent side \(\left(\frac{\text{opposite}}{\text{adjacent}}\right)\). SOH CAH TOA is a popular way to remember these relationships.
Another one of the important tools in right triangle trigonometry is the Pythagorean theorem, which states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. This can be written as \(a^2 + b^2 = c^2\), where \(c\) is the hypotenuse and \(a\) and \(b\) are the legs.
To solve for the acute angles in right triangle trigonometry, it is often necessary to use the inverse trigonometric functions, which are the inverse of the sine, cosine, and tangent functions. These functions are abbreviated as \(\sin^{-1}\), \(\cos^{-1}\), and \(\tan^{-1}\), respectively.
Right triangle trigonometry is used in a variety of fields, including geometry, engineering, and physics. It is also a useful tool for solving real-world problems.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!