Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
Notes
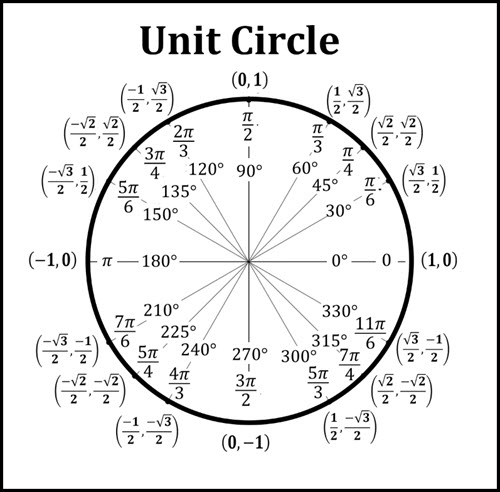
Printable PDF of Unit Circle
Printable Blank Unit Circle
Practice Problems
Find the following trig values on the unit circle.
\(\textbf{1)}\) \(\sin{\displaystyle\frac{2\pi}{3}}\)
\(\textbf{2)}\) \(\sin{45^{\circ}}\)
\(\textbf{3)}\) \(\sin{30^{\circ}}\)
\(\textbf{4)}\) \(\cos{\displaystyle\frac{\pi}{6}}\)
\(\textbf{5)}\) \(\tan{210^{\circ}}\)
\(\textbf{6)}\) \(\tan{\displaystyle\frac{4\pi}{3}}\)
\(\textbf{7)}\) \(\sin{-60^{\circ}}\)
\(\textbf{8)}\) \(\cos{-45^{\circ}}\)
\(\textbf{9)}\) \(\tan{90^{\circ}}\)
\(\textbf{10)}\) \(\sin{\displaystyle\frac{5\pi}{4}}\)
\(\textbf{11)}\) \(\sin{150^{\circ}}\)
\(\textbf{12)}\) \(\tan{225^{\circ}}\)
\(\textbf{13)}\) \(\tan{150^{\circ}}\)
\(\textbf{14)}\) \(\sin{\displaystyle\frac{3\pi}{4}}\)
\(\textbf{15)}\) \(\sin{-210^{\circ}}\)
\(\textbf{16)}\) \(\cos{210^{\circ}}\)
\(\textbf{17)}\) \(\tan{180^{\circ}}\)
\(\textbf{18)}\) \(\sin{90^{\circ}}\)
\(\textbf{19)}\) \(\cos{-\displaystyle\frac{2\pi}{3}}\)
\(\textbf{20)}\) \(\sin{300^{\circ}}\)
\(\textbf{21)}\) \(\tan{-45^{\circ}}\)
\(\textbf{22)}\) \(\tan{-\displaystyle\frac{\pi}{3}}\)
\(\textbf{23)}\) \(\cos{\displaystyle\frac{3\pi}{4}}\)
\(\textbf{24)}\) \(\tan{\displaystyle\frac{5\pi}{3}}\)
\(\textbf{25)}\) \(\cos{-\displaystyle\frac{\pi}{6}}\)
\(\textbf{26)}\) \(\cos{0^{\circ}}\)
\(\textbf{27)}\) \(\cos{315^{\circ}}\)
\(\textbf{28)}\) \(\tan{\displaystyle\frac{\pi}{3}}\)
\(\textbf{29)}\) \(\tan{0\pi}\)
\(\textbf{30)}\) \(\tan{-\displaystyle\frac{7\pi}{6}}\)
\(\textbf{31)}\) \(\tan{\displaystyle\frac{2\pi}{3}}\)
\(\textbf{32)}\) \(\sin{210^{\circ}}\)
\(\textbf{33)}\) \(\cos{90^{\circ}}\)
\(\textbf{34)}\) \(\tan{135^{\circ}}\)
\(\textbf{35)}\) \(\tan{315^{\circ}}\)
\(\textbf{36)}\) \(\cos{-\displaystyle\frac{7\pi}{6}}\)
\(\textbf{37)}\) \(\cos{150^{\circ}}\)
\(\textbf{38)}\) \(\cos{-\displaystyle\frac{\pi}{3}}\)
\(\textbf{39)}\) \(\sin{-45^{\circ}}\)
\(\textbf{40)}\) \(\cos{180^{\circ}}\)
\(\textbf{41)}\) \(\cos{\displaystyle\frac{5\pi}{4}}\)
\(\textbf{42)}\) \(\tan{-30^{\circ}}\)
\(\textbf{43)}\) \(\cos{240^{\circ}}\)
\(\textbf{44)}\) \(\sin{-120^{\circ}}\)
\(\textbf{45)}\) \(\sin{270^{\circ}}\)
\(\textbf{46)}\) \(\cos{300^{\circ}}\)
\(\textbf{47)}\) \(\sin{315^{\circ}}\)
\(\textbf{48)}\) \(\sin{240^{\circ}}\)
\(\textbf{49)}\) \(\tan{30^{\circ}}\)
\(\textbf{50)}\) \(\tan{45^{\circ}}\)
\(\textbf{51)}\) \(\sin{\pi}\)
\(\textbf{52)}\) \(\sin{-30^{\circ}}\)
\(\textbf{53)}\) \(\tan{-120^{\circ}}\)
\(\textbf{54)}\) \(\tan{270^{\circ}}\)
\(\textbf{55)}\) \(\cos{45^{\circ}}\)
\(\textbf{56)}\) \(\sin{0^{\circ}}\)
\(\textbf{57)}\) \(\cos{60^{\circ}}\)
\(\textbf{58)}\) \(\cos{270^{\circ}}\)
\(\textbf{59)}\) \(\sin{\displaystyle\frac{\pi}{3}}\)
\(\textbf{60)}\) \(\cos{\displaystyle\frac{2\pi}{3}}\)
\(\textbf{61)}\) \(\sin{120^{\circ}}\)
\(\textbf{62)}\) \(\cos{30^{\circ}}\)
\(\textbf{63)}\) \(\tan{240^{\circ}}\)
\(\textbf{64)}\) \(\sin{225^{\circ}}\)
\(\textbf{65)}\) \(\sin{135^{\circ}}\)
\(\textbf{66)}\) \(\cos{-120^{\circ}}\)
\(\textbf{67)}\) \(\tan{-60^{\circ}}\)
\(\textbf{68)}\) \(\cos{135^{\circ}}\)
\(\textbf{69)}\) \(\tan{300^{\circ}}\)
\(\textbf{70)}\) \(\cos{-30^{\circ}}\)
\(\textbf{71)}\) \(\tan{60^{\circ}}\)
\(\textbf{72)}\) \(\tan{0^{\circ}}\)
\(\textbf{73)}\) \(\tan{-210^{\circ}}\)
\(\textbf{74)}\) \(\tan{120^{\circ}}\)
\(\textbf{75)}\) \(\cos{-210^{\circ}}\)
\(\textbf{76)}\) \(\cos{-60^{\circ}}\)
\(\textbf{77)}\) \(\cos{225^{\circ}}\)
\(\textbf{78)}\) \(\sin{180^{\circ}}\)
\(\textbf{79)}\) \(\sin{60^{\circ}}\)
\(\textbf{80)}\) \(\cos{120^{\circ}}\)
\(\textbf{81)}\) \(\sin{\displaystyle\frac{5\pi}{6}}\)
See Related Pages\(\)
\(\bullet\text{ Right Triangle Trigonometry}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\displaystyle\frac{\text{opp}}{\text{hyp}}…\)
\(\bullet\text{ Angle of Depression and Elevation}\)
\(\,\,\,\,\,\,\,\,\text{Angle of Depression}=\text{Angle of Elevation}…\)
\(\bullet\text{ Convert to Radians and to Degrees}\)
\(\,\,\,\,\,\,\,\,\text{Radians} \rightarrow \text{Degrees}, \times \displaystyle \frac{180^{\circ}}{\pi}…\)
\(\bullet\text{ Degrees, Minutes and Seconds}\)
\(\,\,\,\,\,\,\,\,48^{\circ}34’21”…\)
\(\bullet\text{ Coterminal Angles}\)
\(\,\,\,\,\,\,\,\,\pm 360^{\circ} \text { or } \pm 2\pi n…\)
\(\bullet\text{ Reference Angles}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
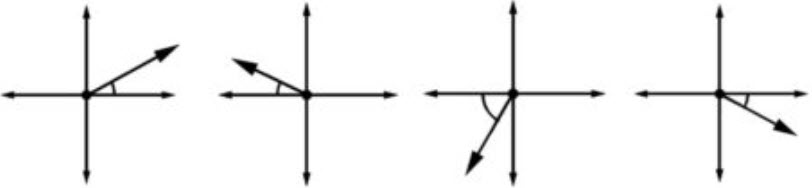\(\bullet\text{ Find All 6 Trig Functions}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
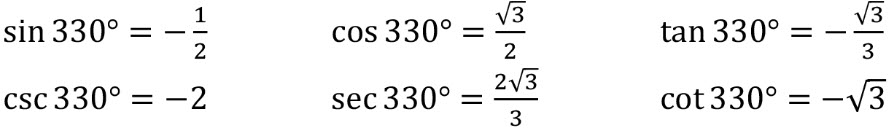\(\bullet\text{ Unit Circle}\)
\(\,\,\,\,\,\,\,\,\sin{(60^{\circ})}=\displaystyle\frac{\sqrt{3}}{2}…\)
\(\bullet\text{ Law of Sines}\)
\(\,\,\,\,\,\,\,\,\displaystyle\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}\)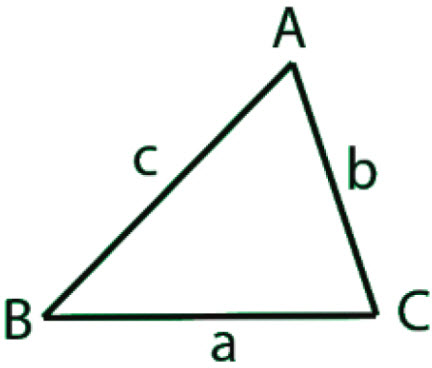 
\(…\)
\(\bullet\text{ Area of SAS Triangles}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\frac{1}{2}ab \sin{C}\) \(…\)
\(\bullet\text{ Law of Cosines}\)
\(\,\,\,\,\,\,\,\,a^2=b^2+c^2-2bc \cos{A}\) \(…\)
\(\bullet\text{ Area of SSS Triangles (Heron’s formula)}\)
\(\,\,\,\,\,\,\,\,\text{Area}=\sqrt{s(s-a)(s-b)(s-c)}\) \(…\)
\(\bullet\text{ Geometric Mean}\)
\(\,\,\,\,\,\,\,\,x=\sqrt{ab} \text{ or } \displaystyle\frac{a}{x}=\frac{x}{b}…\)
\(\bullet\text{ Geometric Mean- Similar Right Triangles}\)
\(\,\,\,\,\,\,\,\,\)
\(…\)
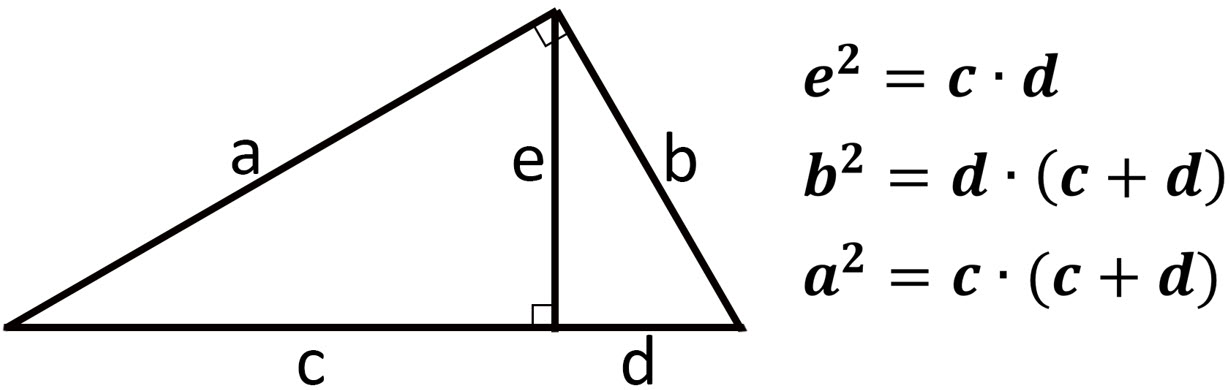\(\bullet\text{ Inverse Trigonmetric Functions}\)
\(\,\,\,\,\,\,\,\,\sin {\left(cos^{-1}\left(\frac{3}{5}\right)\right)}…\)
\(\bullet\text{ Sum and Difference of Angles Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}…\)
\(\bullet\text{ Double-Angle and Half-Angle Formulas}\)
\(\,\,\,\,\,\,\,\,\sin{(2A)}=2\sin{(A)}\cos{(A)}…\)
\(\bullet\text{ Trigonometry-Pythagorean Identities}\)
\(\,\,\,\,\,\,\,\,\sin^2{(x)}+\cos^2{(x)}=1…\)
\(\bullet\text{ Product-Sum Identities}\)
\(\,\,\,\,\,\,\,\,\cos{\alpha}\cos{\beta}=\left(\displaystyle\frac{\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}}{2}\right)…\)
\(\bullet\text{ Cofunction Identities}\)
\(\,\,\,\,\,\,\,\,\sin{(x)}=\cos{(\frac{\pi}{2}-x)}…\)
\(\bullet\text{ Proving Trigonometric Identities}\)
\(\,\,\,\,\,\,\,\,\sec{x}-\cos{x}=\displaystyle\frac{\tan^2{x}}{\sec{x}}…\)
\(\bullet\text{ Graphing Trig Functions- sin and cos}\)
\(\,\,\,\,\,\,\,\,f(x)=A \sin{B(x-c)}+D \)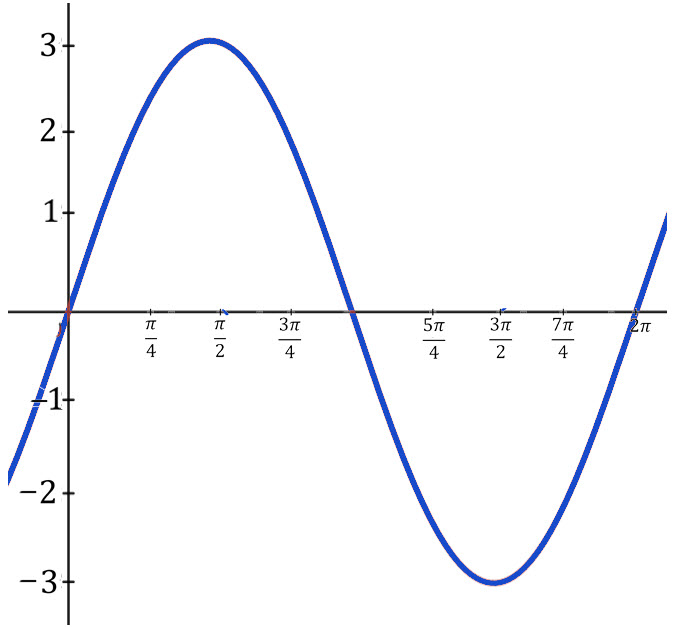 
\(…\)
\(\bullet\text{ Solving Trigonometric Equations}\)
\(\,\,\,\,\,\,\,\,2\cos{(x)}=\sqrt{3}…\)
In Summary
The unit circle is a fundamental concept in mathematics, specifically in trigonometry. It is a circle with a radius of 1 unit, centered at the origin of a coordinate plane. The unit circle is often used to help understand and visualize the relationships between angles and their corresponding trigonometric functions.
An important aspect of the unit circle is the concept of reference angles. A reference angle is the acute angle formed between the x-axis and the terminal side of an angle in the coordinate plane. It is used to simplify the calculation of trigonometric functions for angles that are not acute. The points of interest on the unit circle are the intersections with the x- and y- axis and all possible 30-60-90 and 45-45-90 right triangles that have a reference angle in the circle.
The unit circle helps to understand the concept of radians, which is a unit of measurement for angles. One radian is equal to the length of the arc on the unit circle that is formed by the angle, divided by the radius of the circle. This means that the circumference of the unit circle is equal to 2π radians, where π is a mathematical constant approximately equal to 3.14.
The unit circle can also be used to understand the relationships between the trigonometric functions. For example, the sine and cosine functions have a periodic relationship, meaning that they repeat after a certain interval. This interval is known as the period of the function, and for the sine and cosine functions, the period is equal to 2π.
The unit circle can be a lot of fun once you understand it. Try out the many practice problems on this page to get more comfortable with it.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!